ARCHIVED – PHYS 4C Conceptual Questions

This is an archive of Physics 4C conceptual questions. The last semester these questions (and answers) were used was in Spring 2024 class, and with the recent re-organization of the course material, I don’t anticipate using them again, so this is a kind of “resting place” for this material.

General Instructions

[ARCHIVAL NOTE: Below are the general instructions used at the beginning of the conceptual questions set, under the “Instructions” heading]

This is a peer-graded assignment. After the assignment due date, you will be assigned 3 peer reviews for this assignment. Please follow the instructions in the peer review assignment (which also contains model answers and grading notes) to complete the peer reviews.

The conceptual questions below, some from the textbook and others that relate to the topics covered in the textbook, can mostly be answered adequately in one paragraph or so. If you see more than three questions, you only need to answer up to three questions for a complete submission.

Please answer the following three (3) conceptual questions in your response to this assignment. Use of text box for online submission is highly recommended.

[ARCHIVAL NOTE: Below are the general instructions used at the end of the conceptual questions set, immediately after the last question]

Please click on “Submit” button at the top of this page to submit your answers. Use of text box for online submission is highly recommended (text box has advanced editing options that can meet most needs). Use the file upload option if you have to upload images or PDF for your answers.

[ARCHIVAL NOTE: Below are the general instructions—under the “Instructions” heading—used at the beginning of the “peer review” assignment, which contained the model answers]

After the due date for [LINK to CONCEPTUAL QUESTIONS SET], you should have been assigned up to three classmates’ submissions for peer review. The links to these assignments are available within the page for [LINK to CONCEPTUAL QUESTIONS SET]; look for the links near the portion of the page showing your own submission info, either on the right side of the page or the bottom, depending on the size of your web browser window.

Please review the submissions using the provided rubric; mark the rubric based on the completeness and evidence of effort demonstrated. For a peer review to be considered complete, you must fill out the grading rubric, separately for each submission. I do encourage you to observe how your peers’ submissions compare to your own and leave an encouraging feedback. You can leave comments either within the rubric or outside of the rubric. Do please note that your peers cannot respond to you, as peer review communications only go one way, from the reviewer to the reviewee.

In case it’s helpful, below section provides model answers to the associated conceptual questions.

[ARCHIVAL NOTE: Below are the general instructions—as additional sections—used at the end of the “peer review” assignment]

Late Peer Reviews – There is some limited grace period between the peer review due date and when I assign peer review scores. Beyond this, please note there will be no extensions. Peer reviews must be received on time for them to be useful to the people you are reviewing. If you do not see any peer reviews assigned to you and it’s past peer review deadline, it’s because I removed all incomplete peer review assignments when I gave peer review credit.

“Mark as Done” – You must mark this assignment as done before you can move onto the next item in the Module. In this class, “mark as done” simply means you take responsibility for knowing the information on the page (whereas “view” requirement simply means your web browser accessed the information). So, if you feel you understood what is on this page and you take responsibility, please mark it as done, so that you can move on to the next page.

Rubrics

[ARCHIVAL NOTE: Below are “Conceptual Questions Rubric“, same rubric repeated for Questions 1, 2, and 3]

Conceptual Question 1: Completeness of the response to Conceptual Question 1 (or one of three questions answered)

2 pts – Complete: The response is clearly marked as a response to Conceptual Question 1 (or one of three questions answered) and demonstrates a good-faith effort at answering the question.
1 pts – Incomplete: The response is not clearly marked as responding to Conceptual Question 1 (or one of three questions answered) and/or good-faith effort at answering the question is not evident.
0 pts – No response: No response can be matched up to Conceptual Question 1 (or one of three questions answered).

[ARCHIVAL NOTE: Below is “Peer Review Rubric”]

Completeness: Completeness of peer reviews with evidence of effort.

3 pts – Complete: All three assigned peer reviews have been completed with a clear evidence of effort shown.
2 pts – Incomplete: One or more of peer reviews have not been completed, and/or lack of good-faith effort in the completed peer review(s) is evident.
0 pts – No reviews: None of the three assigned peer reviews have been completed in a meaningful way.

Introduction to Optics (questions and model answers)

Q1 – The accepted value of speed of light is exactly 2.99792458 x 10⁸ m/s. There are very few exact physical constants (by “exact,” we mean this number has infinite significant figures, as in speed of light is 2.99792458000000 (and so on) x 10⁸ m/s. Explain how speed of light came to be accepted as this exact value.

A1 – “Exact value of c“: Speed of light (more generally electromagnetic wave) is related to fundamental electric and magnetic constants by the relationship, $c=1/\sqrt{\epsilon_0 \mu_0}$ . Although the SI unit of meter was originally determined in relation to the dimensions of Earth (being defined as 1/10,000,000 of the distance between the North Pole and the equator), over the years, improvements in precision measurements made the uncertainties in this definition (tied to uncertainty in measuring the distance between the North Pole and the equator) unacceptably large. For a time, meter was defined using an artifact, that is, an object defined to be a “standard meter” (the object was carefully kept and copies were made and sent out to all the countries for use as reference). After a series of re-definitions, in 1983, the definition of meter was fixed by defining the speed of light to be the quoted exact value (then the combination of speed of light with the precise definition of “second” using the atomic clock standard (chosen in 1967) gives what a meter is, as precisely as we can measure the speed of light). (Wikipedia reference). [An aside: recently, the kilogram has been re-defined similarly, by fixing another physical constant, “Planck’s constant” (that you will see later this semester), as an exact value.]

Q2 – [OpenStax, Ch. 1, Question 2] Why is the index of refraction always greater than or equal to 1?

A2 – “Why always n > 1?“: Because the speed of light in vacuum, c, is fastest the light travels (or, for that matter, anything travels, as you will see when we cover special relativity). Since n = c/v, and speed of light in matter, v, is always smaller than c, index of refraction is always greater than 1. [An aside: Having said all this, there is something called “anomalous dispersion” or “anomalous refraction” which causes index of refraction to be smaller than 1. This usually happens around absorption resonance and would be covered in a class dealing with nonlinear optics.]

Q3 – Compare and contrast laws of reflection and refraction. What laws of optics (describe it in words or write down an equation) tell you how to predict the direction of reflected rays? The direction of refracted rays?

A3 – “Compare and contrast reflection and refraction“: Reflection describes how a ray of light, after striking a smooth surface, bounces off (on the same side as incoming rays). Refraction describes how a ray of light, when incident on a transparent material, is transmitted through the transparent material. For example, when a laser beam strikes a water (or glass) surface, both reflection and refraction occur. Reflection is described by law of reflection, which says angle of incidence (angle between incident ray and the perpendicular to the surface) is equal to the angle of reflection (angle between the reflected ray and the perpendicular to the surface, on the same side as incident ray). Refraction is described by Snell’s law, which says, for a light ray being transmitted from medium of index of refraction n₁ to n₂, the angle of incidence (θ₁) is related to the angle of refraction (θ₂) in this way: $n_1 \sin \theta_1 = n_2 \sin\theta_2$ .

Q4 – [OpenStax, Ch. 1, Question 13] How can you use total internal reflection to estimate the index of refraction of a medium?

A4 – “Measure n with TIR“: The critical angle at which total-internal reflection happens is related to the index of refraction of the material. So, this would be a possible arrangement: shine a beam of light on a prism (of unknown index of refraction n), rotate the prism until total internal reflection (TIR) just barely happens on the outgoing face of the prism. The angle of incidence on that face of prism is related to the index of refraction by: $\theta_\mathrm{crit} = \arcsin(1/n)$ , where 1 is index of refraction of air and n is the index of refraction of the material. (Some geometry may be necessary to relate the angles that can be measured outside the prism to the angle of incidence that is inside the prism.)

Q5 – [OpenStax, Ch. 1, Quesion 20] No light passes through two perfect polarizing filters with perpendicular axes. However, if a third polarizing filter is placed between the original two, some light can pass. Why is this? Under what circumstances does most of the light pass?

A5 – “Light transmitted through polarizers“: Malus’ law says that $I_\mathrm{trans} = I_0 \cos^2 \theta$ for a perfect polarizer (this is based on the property of the polarizer, that it allows the component of electric field oscillating in a particular direction to be transmitted, while blocking the other component). So, if two polarizers are at 90 deg to each other, since cos(90 deg) = 0, the transmitted intensity will be zero. However, if a new polarizer is placed between these two polarizers, than the angle between adjacent polarizers do not have to be 90 deg (for example, angle between first and second polarizer could be 20 deg, and the angle between the second and third polarizer would be 70 deg). This makes it possible for some intensity to be transmitted, since $\cos^2(20^\circ)\times\cos^2(70^\circ)\neq 0$ . If you try plugging in numbers, you will see that the arrangement that makes the most light pass through is if the second polarizer is at 45 deg from both the first and the third polarizer, so that transmitted intensity is $\cos^2(45^\circ) \times \cos^2(45^\circ)=1/4$ of the incident light.

Optics Applications (questions and model answers)

Q1 – Explain why a plane mirror always forms a virtual image. What makes the image formed by a plane mirror “virtual”?

A1 – “Why a plane mirror always forms a virtual image“: A plane mirror always forms a virtual image because the light rays coming from the mirror after reflection appear to come from a point behind the mirror. So the light rays do not actually go through the image, they only appear to come from the image, and this makes the image by a plane mirror virtual. [A second, slightly more quantitative response: the light rays from a real object will be diverging as they are incident on the plane mirror. Since the light rays all reflect out at the same angle as incident angle, the light rays continue to diverge after reflecting from the plane mirror, and since they never converge on the outgoing side, they do not form a real image (on the outgoing side) but instead form a virtual image (on the opposite side to the outgoing side).]

Q2 – Answer the following series of questions and explain your response:

[OpenStax, Chapter 2, Question 2] Can you see a virtual image?
[OpenStax, Chapter 2, Question 3] Can you photograph a virtual image?
[OpenStax, Chapter 2, Question 4] Can you project a virtual image onto a screen?
[OpenStax, Chapter 2, Question 5] Is it necessary to project a real image onto a screen to see it?

A2 – Short series of Q&A:

“Can you see a virtual image?” Yes, you can. The light rays appear to come from the virtual image (meaning you can see the light rays and where they appear to come from).
“Can you photograph a virtual image?” Depends. If the question means “Can you place a film at the location of a virtual image and expect the film to record the virtual image,” the answer is no. If the question means “Can you take a picture of a virtual image with a camera?” (for example, think of a selfie taken on a mirror) then yes. There are real light rays that do appear to come from the virtual image, and these real light rays can be used to make a photograph (the lens system in a camera would use these light rays from a virtual image to form a final real image which is formed on the film or CCD. [Both answers here are defensible, but the second reading is stronger, especially given the next question.]
“Can you project a virtual image onto a screen?” No. To project an image, you need real light rays coming to a focus at the location of the screen. Since the light rays from a virtual image only appear to come from the virtual image (they don’t actually come from or go through the virtual image, so when you place the screen at the location of the virtual image, there are no real light rays that come to focus at that location.
“Is it necessary to project a real image onto a screen to see it?” No. Take out a magnifying glass, hold it far from you and point it at faraway objects. You will see the images of these objects upside down through the magnifying glass, and these are real images.

Q3 – What is “spherical aberration” in a curved mirror made for imaging (forming a real image on a CCD sensor, for example, to take an astronomical photo)? Explain the reason for this aberration and what may be done to avoid it.

A3 – “Spherical aberration“: Spherical aberration comes from the small-angle approximation used in the derivation of the focal length of a curved mirror in terms of its radius of curvature. The exact expression for focal length of a spherical mirror depends on the angle of incidence (for parallel rays, this is determined by how far away the ray is from optical axis), meaning not all rays come to focus at the same point, and this defect gets worse (i.e. the approximation is not as good) the farther away the rays are from the optical axis. There are two main ways to avoid the distortion due to spherical aberration: (a) use a small mirror (so that all your rays incident on the mirror are very close to the optical axis, compared to the mirror’s radius of curvature), and/or (b) use a parabolic shape for the mirror (which has no angle-of-incidence dependence even for exact expression for the focal length).

[An Aside: Similar note applies to lenses—except lenses suffer also from something else called “chromatic aberration.” The photo below shows how, for a parabolic lens, high-quality image is formed right up to the edge of a large-diameter, short-focal-length lens.]

Q4 – [OpenStax, Chapter 2, Question 14] You can argue that a flat piece of glass, such as in a window, is like a lens with an infinite focal length. If so, where does it form an image? That is, how are d_i and d_o related?

A4 – “Image of a flat glass“: A thin flat glass forms a virtual image at the same location as the object. That is, an object that you look through a thin flat glass looks like it is at the location of the object (that makes sense, doesn’t it?). Here’s a more mathematical approach to prove it. From the thin-lens equation, $1/d_o + 1/d_i = 1/f$ , if we let $f \to \infty$ , then 1/f becomes zero, and we have 1/d_o = -1/d_i, or, d_i = -d_o. That is, we have a virtual image (formed on the opposite side of outgoing rays; in this case, this describes the side the object is on), at the same distance away as the object. So, we have a virtual image at the same physical location as the object.

Q5 – Compare and contrast images formed by reflection with images formed by refraction. Name at least 3 distinct features, with at least one feature in each category of “compare” and “contrast.”

A5 – “Compare/contrast image formed by reflection/refraction“: [Note for the grader: if someone mentions at least two significant things, they should receive full credit] There are a number of things one can mention. Here are some of them, in no particular order:

Both images formed by reflection and refraction can suffer from spherical aberration.
Only image formed by refraction is affected by chromatic aberration.
Real image formed by reflection is on the same side as the real object; real image formed by refraction is on the opposite side of the real object.
Real image forms on the side of outgoing rays, both for image formation by reflection and by refraction.
Image formation by reflection depends only on geometric parameters, like radius of curvature; image formation by refraction also depends on material properties, like index of refraction.
A “converging” arrangement in case of reflection is given by concave mirrors; a “converging” arrangement in case of refraction usually involves a lens with a convex surface.
In image formation by reflection, the virtual image forms on the side that never has any light rays (incoming or outgoing); in image formation by refraction, the virtual image forms on the same side as the incoming light rays.
… and there’s probably more.

Q6 – [OpenStax, Chapter 2, Question 20] Why is your vision so blurry when you open your eyes while swimming under water? How does a face mask enable clear vision?

A6 – “Blurry vision underwater“: This can be explained using lensmakers’ formula, which gives the focal length of a lens: $\frac{1}{f} = \left(\frac{n_2}{n_1} -1\right)\left(\frac{1}{R_1} - \frac{1}{R_2}\right)$ where, in particular, n₁ is the index of refraction of medium outside the lens, and n₂ is the index of refraction of the medium that the lens is made of. As you can see, the closer n₁ gets to n₂ (usually n₂ > n₁), the smaller the value of 1/f becomes, which means focal length f becomes longer. With a longer focal length, images form farther away, and it becomes harder for the lens of the eye to form focused real image on retina of the eye, meaning your vision becomes blurry. A face mask enables clear vision by making sure n₁ outside the lens of the eye is 1 (air), so that the focal length of the eye is appropriate for the distance between the lens of the eye and the retina.

Interference (questions and model answers)

Q1 – [OpenStax, Chapter 3, Question 3] Why won’t two small sodium lamps (each producing monochromatic light of lambda=589 nm), held close together, produce an interference pattern on a distant screen? What if the sodium lamps were replaced by two laser pointers held close together? (Note: For the purpose of this question, assume that you can hold the two lamps/two laser pointers as close to each other as necessary.)

A1 – “Interference pattern by sodium lamps vs. lasers“: This question concerns the phase coherence, or simply coherence. Most natural light sources are “incoherent,” meaning that there is no consistent phase description for the electromagnetic waves coming from the light source. Despite the continuous train of sine wave you have seen drawn in lecture, a more accurate picture would be broken trains of short sine waves (each one lasting a fraction of a microsecond), with one train having no fixed phase relationship with other trains. Since interference phenomenon relies on phase difference between two wave sources, if you have two wave sources that are incoherent, like two sodium lamps, any interference pattern between them would be momentary and quickly washed out constant fluctuations in the pattern. With two coherent wave sources, like lasers (this is one of the special properties of lasers; we will cover more later), interference pattern would remain stable and be visible. [Having said that, Young’s double-slit experiment was done before the invention of lasers. By having a single slit before the double-slit, you can ensure that the relative phase of light arriving at the two slits are the same (they are in phase), even though the their phase compared to at other times is varying at random.]
Also for those interested, please take a look at below extended remarks about stabilizing lasers (my apologies for the video/audio quality; my computer was having some issues):

Q2 – [OpenStax, Chapter 3, Question 5] Why is monochromatic light used in the double slit experiment? What would happen if white light were used?

A2 – “Why monochromatic light?“: Monochromatic light is used since color relates to the wavelength of light, and in obtaining the phase difference between light from two slits, there is a dependence on the wavelength of light. So the interference pattern for a red light (633-nm wavelength, for example) would be broader than the interference pattern for a blue light (about 400-nm wavelength). For a consistent location of interference maxima and interference minima, a light source of a single wavelength should be used. If white light (combination of light wavelengths ranging from 400 nm to 700 nm) is used, you would see all the interference patterns simultaneously. Depending on the sharpness of interference peaks and valleys, you might see rainbow colors, or you might not notice any apparent changes in intensity.

Q3 – [OpenStax, Chapter 3, Question 7] How is the difference in paths taken by two originally in-phase light waves related to whether they interfere constructively or destructively? How can this be affected by reflection? By refraction? (Hint: What is important for obtaining constructive/destructive interference: difference in the physical path length between two paths, or some other quantity, which is affected by the physical path length, as well as a few other considerations? Review Section 3.4, if necessary.)

A3 – “Path-length difference“: For the simple double-slit interference setup (only the path-length difference affecting the phase difference, no reflection/refraction), the path-length difference and constructive/destructive interference is simply and intuitively related: (1) for constructive interference, path-length difference must be an integral number of wavelength, so that the two light waves starting out in phase arrive in phase, and (2) for destructive interference, path-length difference must be a half-integer number (that is, 0.5, 1.5, 2.5, etc.) of wavelength, so that the two light waves starting out in phase arrive out of phase. Following are the rules to remember in considering interference of light that undergoes reflection/refraction:

For reflection, the reflection introduces a 180-degree phase shift when the light is reflecting from a medium of higher index of refraction (this is something that is proven in upper-division electrodynamics). So, for example, reflection of light going from air (n=1) to water (n=1.33) results in 180-degree phase shift, but reflection of light going from water to air does not result in any phase shift.
For refraction, you simply need to account for the change in wavelength (according to v=c/n and λ=v/f, so λ=λ₀/n, where λ₀ is wavelength of the light in vacuum), and remember what matters is the relative phase, given from path-length difference as a fraction of the wavelength.

Q4 – The debate between proponents of wave theory of light and non-wave theory of light is a long and historical one. It goes as far back as 17th and 18th centuries (time of Newton), before Young’s double-slit experiment (done in early 19th century) put the question to rest. What is interesting here is that Newton was a proponent of a non-wave theory of light (called “corpuscular theory of light”), and yet, he is credited for analyzing an interference phenomenon seen with reflection of light from lens placed on a flat glass, called “Newton’s rings” (see photo below). How did Newton explain this experimental phenomenon that he analyzed (and is credited for)? [You may need to do some research on your own; Wikipedia is generally reliable on topics that relate to lower-division math and physics.]

A4 – “Newton’s Rings“: [Note for the grader: This question addresses topics outside of your textbook reading, so expect a wide range in quality of responses.] It is a peculiar historical oddity. Newton is known for his advocacy of non-wave theory of light (“corpuscular theory of light“), and yet, he is also known for his analysis of a wave-interference phenomena that we today call “Newton’s Rings.” Without going into too much history (physicists don’t make good historians, anyway), a key aspect of this history to understand is the fact that Newton’s theory was more complex than how many of his contemporaries understood it. You can get a glimpse of this complexity when you look at how he tried to describe the phenomenon of reflection (partial reflection on incidence on a transparent medium is yet another aspect of light that was more naturally explained by the wave theory; read more about his “theory of fits“). In the end, his major contribution to this phenomenon (and why we call it “Newton’s Rings,” not “Hooke’s Rings” or “Young’s Rings”) is he gave a quantitative description of the relationship between the thickness of air gap (in the case of a lens sitting on a glass plate) and rings of color. [P.S. Please don’t read too much into comparison between Newton’s corpuscular theory of light and later Einstein’s theory of photon. With enough retrospective look, you could make Plato out to be a brilliant physicist ahead of his time—which he wasn’t.]

Single-Slit Diffraction (questions and model answers)

Q1 – [OpenStax, Chapter 4, Question 2] Compare interference and diffraction. Specifically, define what is meant by “diffraction”, and distinguish diffraction from interference. [Note: The truth is, even trained physicists often use the word “diffraction” sloppily. For extra, try to identify different ways the word “diffraction” is used in different phrases. In particular, consider the phrases “single-slit diffraction pattern” and “diffraction grating,” among others.]

A1 – “Interference vs. diffraction“: Strictly speaking, “interference” refers to features seen when two or more waves overlap (and combine according to superposition principle). “Diffraction” refers to the spreading of waves seen, when they go through a narrow opening. However, using Huygens’ principle, you can understand diffraction as resulting from interference between Huygens wavelets (each point on wave front considered as a point source of wave). So, what we call single-slit diffraction is also a result of interference (between Huygens wavelets). This interchangeable (or “sloppy”) use of diffraction is clearest in the device called “diffraction grating,” which is really an N-slit interference device (to be covered next week).

Q2 – Conceptually explain the trick used to calculate the locations of single-slit diffraction minima. In English (that is, without using phasor diagrams or complicated integrals), explain how to derive the expressions for the location of the first-order diffraction minimum ( $a \sin\theta = \lambda$ , where a is slit width, λ is wavelength, and θ is the angular position of minimum) and the second-order diffraction minimum ( $a \sin\theta = 2\lambda$ ).

A2 – “Single-slit diffraction minima“: The trick is to find pairs of Huygens wavelets that destructively interfere and use such pairs to cover the whole slit. For the first-order diffraction minimum, you find a spot on the screen such that the Huygens wavelet from the top of the slit and halfway down the slit destructively interfere (see (b) in figure below). And as you move the point at the top down, covering the top half of the slit, the paired part that destructively interferes covers the bottom half of the slit. For the second order minimum, the slit is divided into quarters (see (d) in figure). The Huygens wavelet from the top of the slit and a quarter-way down the slit destructively interfere, and these pairs together cover the top half, as you move the top wavelet down a quarter. You repeat this process for the bottom half of the slit (zero intensities added however many times is still zero).

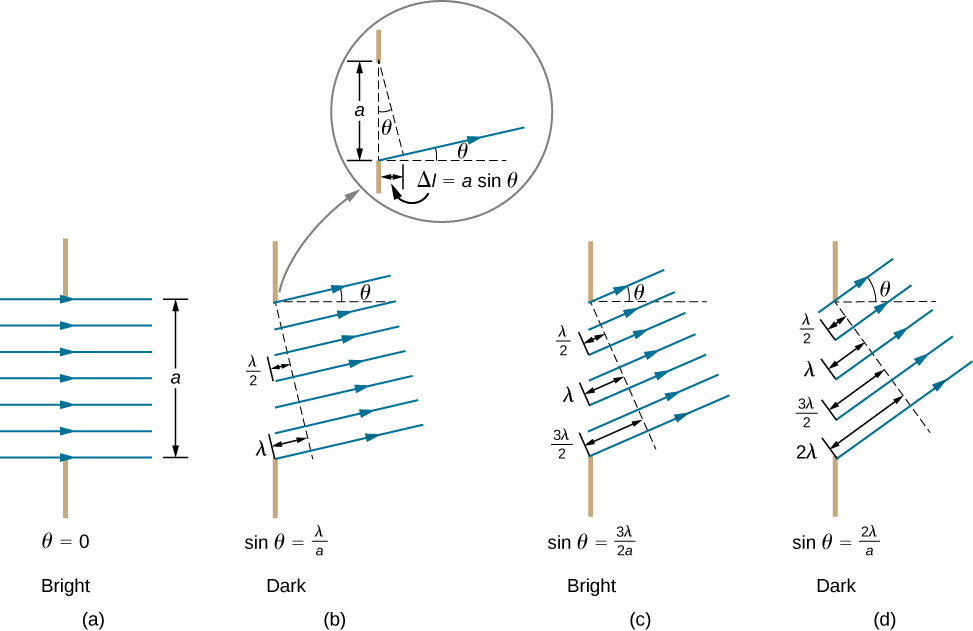
Q3 – [OpenStax, Chapter 4, Question 7] In Equation 4.4, the parameter β looks like an angle but is not an angle that you can measure with a protractor in the physical world. Explain what β represents.

A3 – “Meaning of β“: It’s a phase angle. It is a type of angular quantity which is associated with cycles (cyclical motion like oscillations, waves, and other things). This quantity is used to indicate whether two disturbances from periodic sources will constructively interfere (in the case of double-slit interference, integer multiples of 2π) or destructively interfere (in the case of double-slit interference, π plus integer multiples of 2π). [Note: The exact math for single-slit is more complicated; it’s when β is integer multiples of π that you get destructive interference, and for the exact location for single-slit diffraction maxima, well, you have to use calculus.]

Interference and Diffraction Applications (questions and model answers)

Q1 – Consider the interference pattern for n-slit interference, with n being an integer equal to or greater than 2 (Figure 3.10 from OpenStax on right shows interference pattern for up to 4 slits). Qualitatively describe the changes that occur to the interference pattern as the number of slits is increased (while the distance between the adjacent slits are kept the same). Qualitatively explain why these changes to the interference pattern occur.

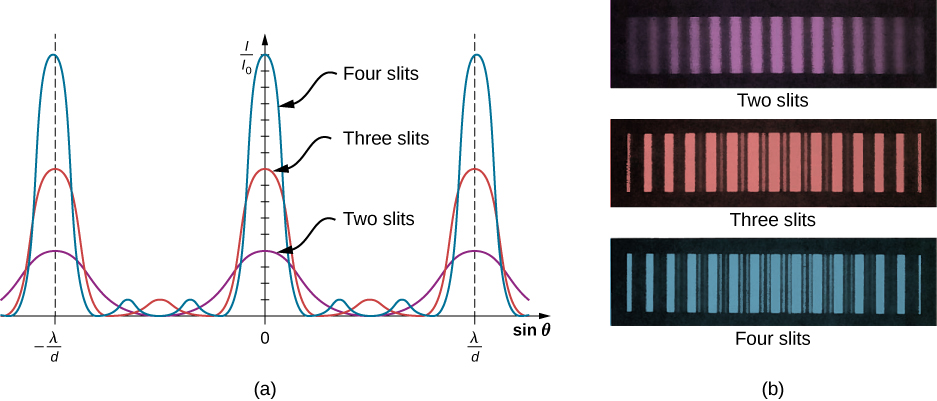
A1 – “n-slit Interference“: With multiple slits, following is what you see in the figure: (1) the most prominent maxima (“principal maxima”) remain at the same location, and (2) there are now more than one place between principal maxima where destructive interference occurs, with the overall result that the bright fringes become more sharply defined. Qualitatively, you can explain this by pairing up the slits that are constructively interfering or destructively interfering: (1) the principal maxima result in locations where neighboring slits constructively interfere, and as you add more slits, neighboring slits continue to constructively interfere at the same location, so the position of principal maxima does not change (and you keep adding more intensity with more slits open), (2) at the midpoint between the principal maxima are where neighboring slits destructively interfere, so you still have interference minima there, but in addition (3) when you pair up every other slit (or every third slit, or every n-th slit) to destructively interfere, the overall result is that you still end up with destructive interference for the whole collection of slits—this is where the additional interference minima between the principal maxima come from.

Q2 – Are the features visible in the spectrum of a diffraction grating resulting from interference or diffraction? Explain your answer. What aspect of the spectrum can be attributed to diffraction (as in “single-slit diffraction”)? [Note: You may wish to review the background material in Lab: Diffraction and Interference [linked to lab manual in course site].]

A2 – “Diffraction grating“: The features seen in the spectrum of a diffraction grating are due to interference, specifically N-slit interference (where N is very large). At a limit of large N, you could think of the width of the principal maxima as arising from single-slit diffraction. The interference minimum closest to the principal maximum would be associated to the first slit being paired with (N/2)th slit for destructive interference (and the second slit with (N/2+1)th slit, etc.), which is a similar argument made for single-slit diffraction. So, if a beam incident on a diffraction grating is wider, the width of principal minimum would be narrower.

Q3 – [OpenStax, Chapter 4, Questions 9 and 11] Answer the following two questions addressing related concepts: (a) Is higher resolution obtained in a microscope with red or blue light? Explain your answer. (b) The distance between atoms in a molecule is about 10^-8 cm. Can visible light be used to “see” molecules?

A3 – “Diffraction-limited resolution“: (a) Higher resolution is obtained with blue light, because according to the Rayleigh criterion ( $\theta_\mathrm{min} = 1.22\lambda/D$ ), the minimum resolvable angle is proportional to the wavelength of light. (b) Visible light cannot be used to “see” molecules. Thinking of distance between the molecules like opening of a single-slit, the diffraction of the visible light is too great to leave any discernable features. In order to “see” molecules, wavelength of light used needs to be comparable to the spacing between the atoms. (As a side note, this is one of the uses of X-ray laser sources like the Advanced Light Source.)

Q4 – [OpenStax, Chapter 4, Question 10] The resolving power of refracting (or reflecting) telescope increases with the size of its objective lens (or mirror). What other advantage is gained with a larger lens (or mirror)?

A4 – “Advantages of larger lens“: In addition to larger resolving power (smallest resolvable angle being given by $\theta_\mathrm{min} = 1.22\lambda/D$ , where D is the diameter of the lens), a larger lens has a bigger area (for circular lens, $A = \pi(D/2)^2$ ), so it collects more light for image formation, meaning fainter sources of light can be seen. (For larger angular magnification, you need a longer focal length, which could be associated with a larger lens, but not necessarily.)

Special Relativity Introduction (questions and model answers)

Q1 – [OpenStax, Chapter 5, Question 2] Is Earth an inertial frame of reference? Is the sun? Explain your answer and describe the approximation we make (usually) in order to be able to consider Earth as an inertial frame of reference.

A1 – “Inertial frame of reference“: Strictly speaking, Earth is not an inertial frame of reference, because it is accelerating: it orbits the Sun in a roughly circular path, and as you learned in Physics 4A, whenever an object is moving in a circular path, there is centripetal acceleration involved. So Earth’s reference frame is technically an accelerating frame and not an inertial reference frame. And the same holds for the Sun also, because the Sun (and the entire solar system) is orbiting about the center of the Milky Way Galaxy (and the entire Milky Way Galaxy is orbiting about the center of our local cluster, and so on—you have to go to pretty large scale astronomically before you can say, “These things are not gravitationally bound to each other and they are not orbiting around something”). Having said all that, there are at least two things you can do to consider Earth as an inertial reference frame. In the order of preference: (1) Earth is approximately an inertial reference frame (deal with situations where either centripetal acceleration of Earth toward the Sun is negligible, or the orbital velocity of Earth (and its variation over 1 year) is negligible compared to velocity of things involved). (2) Consider Earth as a “momentarily co-moving inertial reference frame” (a phrase sometimes used in upper-division or graduate-level courses dealing with special relativity or related subjects [Ref. 1 and Ref. 2 of usage online]). In case of Option (2), you will likely also need to introduce a pseudoforce associated with the acceleration of the reference frame, in order to be able to treat it as an inertial reference frame, one in which Newton’s First Law holds.

Q2 – [OpenStax, Chapter 5, Question 5] Consider a physical/chemical/biological process which typically occurs over a known duration (such as a person aging over decades). To whom does the elapsed time for the process take longer, an observer moving relative to the process, or an observer moving with the process? Which observer measures the interval of “proper time”?

A2 – “Time dilation and proper time“: The elapsed time of the process takes longer for an observer moving relative to the process. That is, if you have a person who would have died of old age in 80 years, for an observer moving relative to the process, this person would die of old age in a time longer than 80 years. The observer who is at rest relative to the process measures the “proper time” for this process. For example, for a space-born astronaut who dies at 80 years old constantly moving at speed of $v=0.866c$ ( $\gamma=2$ ) relative to Earth, the death of the astronaut occurs 160 years after their birth, from an Earth-based observer’s perspective.

Q3 – The fact that cosmic ray muons (created in the upper atmosphere, about 15 km above the surface of Earth) can be detected at sea level despite its short lifetime (about 2 microseconds) is often cited as an evidence of time dilation. Describe these same events (creation of muon in the upper atmosphere and their detection at sea level) from the perspective of muon. What relativistic effect do you need to take into account? Assume that the speed of cosmic ray muon is about $v=0.995c$ .

A3 – “Cosmic ray muons from their perspective“: In the reference frame of cosmic ray muons, they only live for about 2 microseconds (they measure proper time for the muon decay time). So during that time, if the muons move at the speed of $v=0.995c$ (from Example 5.3) relative to Earth, they only move the distance of $d=(0.995c)\times(2\times 10^{-6}\ \mathrm{\mu s})\approx 600\ \mathrm{m}$ (or more accurately, the background moves distance of 600 meters, since the muons are at rest in this reference frame). However, in the muon reference frame, the distance of 15 km (from upper atmosphere to sea level) is length contracted, so that the background only needs to move a distance of $L = L_p/\gamma = 1,500\ \mathrm{m}$ ( $\gamma = 10$ for $v = 0.995c$ ) for the muon to reach the sea level from atmosphere. (Note: 1500 m is still greater than 600 m, but muon decay follows the exponential decay law, and a substantial fraction of original population survives after traveling for about the 3 times the lifetime—the same cannot be said for muons that had to travel for 30 times its lifetime.)

Q4 – [OpenStax, Chapter 5, Question 8] If postulates of special relativity are generally applicable laws of physics and relativistic effects such as time dilation and length contraction are always present (for example, cars and airplanes that we encounter in our everyday lives), why have we not noticed these effects before? Why do special relativistic effects seem strange to us?

A4 – “Lack of special-relativistic intuition“: We have not noticed these effects before, because the speed at which things need to move for relativistic effects (time dilation and length contraction) to become significant is very high. For example, sound moves at speed of 340 m/s (under normal conditions). With something moving at speed of sound (“mach 1”), the Lorentz factor is $\gamma = 1 + 6.4\times 10^{-13}$ (that is, you need to measure length or time with accuracy about 1 part in a trillion to start to see these effects). Having said that, people have done some of these measurements with this level of incredible accuracy to verify the predictions of special relativity, even in our low-speed, everyday life (read more on Wikipedia). But this does explain why our intuition (formed on the basis of our everyday experiences) often disagrees with special-relativistic predictions. (And if you happen to work in high-energy particle physics, you will see confirmation of predictions of special relativity, particularly time dilation, in your “everyday work.”

Lorentz Transformation (questions and model answers)

Q1 – [OpenStax, Chapter 5, Questions 9] Suppose an astronaut is moving relative to Earth at a significant fraction of the speed of light. Please answer and explain.

Does he observe the rate of his clocks to have slowed?
What change in the rate of earthbound clocks does he observe?
Does he measure the length of his ship to be shorter?
Does he measure the distance between two stars that lie in the direction of his motion (for example, distance between Sol and his destination star) to shorten?
Do he and an earthbound observer agree on his velocity relative to Earth?

A1 – “Relativistic astronaut“:

He does not observe his clocks to have slowed (his own clock is at rest relative to him; it’s not a “moving clock” to him).
He observes the earthbound clocks to have slowed (because in his reference frame, the earthbound clocks are moving, and moving clocks are slow).
He does not measure the length of his ship to be shorter (his own ship is at rest relative to him; it’s not a “moving ruler” to him).
He measures the distance between two stars (for example, between Sol and his destination star) to be shorter, consistent with Lorentz contraction. In fact, this is how you would get an agreement between earthbound observer and the astronaut on how he reaches a star—for example, 800 lightyears away—within his own lifetime: earthbound observer observes astronaut’s clock slowing down (so he hardly ages as he takes 800+ years to reach the star), but the astronaut observes the distance shorten (so he is able to reach the star within 80 years or so that he lives, as he travels at a speed close to the speed of light).
Yes, they agree. If the astronaut is moving at 0.99c relative to Earth, the earthbound observer sees the astronaut moving away from Earth at 0.99c, and the astronaut sees Earth moving away from him at 0.99c. Either way, they agree that Earth and the astronaut are moving relative to each other at 0.99c.

Q2 – Suppose an astronaut travels to a star 10 lightyears away at a significant fraction of the speed of light (for example, $v=0.99c$ ) and returns. Assume negligible amount of time is spent at the destination.

Does this round-trip journey take less than, equal to, or more than 20 years as observed by an Earth-based observer?
Does this round-trip journey take less than, equal to, or more than 20 years as observed by the astronaut?

A2 – “Relativistic astronaut, take two“:

The round-trip journey takes more than 20 years. For an Earth-based observer this is simple math that doesn’t involve any special relativity. The round-trip distance is 20 lightyears and the astronaut travels at a speed less than light speed. Therefore, the time ( 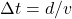$\Delta t = d/v$ ) taken is greater than 20 years. As a general rule, if there is no shift of reference frame, no special relativity needs to be involved.
From previous question, you know the round-trip journey takes less than 20 years for the astronaut. The quickest, self-consistent way to answer this is through length-contraction: in the astronaut’s reference frame, the distance between Earth and the star are length-contracted to a distance less than 20 lightyears, so the round-trip travel can be done in less than 20 years while traveling (more precisely, the “background moving”) at speed less than speed of light. (Answering this through time-dilation is somewhat more convoluted, as there is no way to use time-dilation argument without referring to the Earth observer’s clock—but we are talking about astronaut’s perspective here.)

Q3 – [CHALLENGE QUESTION] For an astronaut traveling to a star 10 lightyears away at $v=0.99c$ and returning, spending negligible amount of time at the destination, describe the journey as the astronaut would observe it. In particular, describe what the astronaut would observe as happening on Earth during the journey. [Note: to simplify the “observation”, you may assume that astronaut has access to a magic telescope—call it ansible—that allows for instantaneous communication.]

A3 – “Relativistic astronaut, take-two description“: [If you got this part completely right, then congratulations—you have understood special relativity; a feat not all students graduating with physics bachelor’s degree achieve.]
(A) As the astronaut approaches the star at near lightspeed (the 10-ly distance length-contracted to 1.4 ly, if the speed is $v=0.99c$ ), the Earth clock is observed to have slowed down. This means all processes happening on Earth happens slower, as observed by the astronaut. In fact, in 1.4 years (the time it takes for the astronaut to reach the distant star), only a few months (0.2 year) have passed on Earth. (B) As the astronaut comes to a stop at the distant star, the astronaut’s sense of simultaneity shifts. If the astronaut observes Earth while coming to a stop, the Earth basically “skips time”, as 9.8 years’ worth of events happen in an arbitrarily short amount of time (basically however long it takes for the astronaut to decelerate to a frame of relative rest to Earth). (C) As the astronaut heads back towards Earth, the astronaut’s sense of simultaneity shifts again. In an arbitrarily short amount of time, 9.8 years’ worth of events happen on Earth (as the astronaut observes through the magic telescope), setting up the stage for the final leg of the journey. (D) The astronaut returns to Earth in 1.4 years (ship time), and during that time, time-dilated Earth clock counts 0.2 year. And on return, everything is consistent with everything else: the astronaut spent only 2.8 years, and the Earth clock did count about 20 years total, and the astronaut can account for everything that happened on Earth, including the 19.6 years’ worth of time-skip (remember only 0.4 year of Earth time passes during transit, due to time-dilation effect as observed from the astronaut’s reference frames) that occurs during the deceleration/acceleration of the spaceship.

Relativistic Dynamics (questions and model answers)

Q1 – [OpenStax, Chapter 5, Question 14] Special Relativity represents what is known as “paradigm shift” among philosophers of science. That means potentially, everything you thought you knew about physics might have to change (although we hope we can still salvage some). Let’s try to be careful in throwing out the bath water (and not the baby). Please answer following questions:

How does special relativity affect the following general principles of physics you have learned so far? Explain your response: principle of relativity (laws of physics not dependent on inertial reference frame), conservation of energy and momentum, calculation of relative velocity, and principle of inertia (i.e. Newton’s First Law).
How does special relativity affect the application of general principles of physics? In particular, answer for: conservation of energy and momentum, and calculation of acceleration of a body under a force.

A1 – “Paradigm shift with special relativity“:

In most cases, special relativity does not change the general principles of physics. Specifically answering what was asked: (1) principle of relativity still holds (this, in fact, is the first postulate of special relativity), (2) conservation of energy and momentum is still valid (provided you use relativistically correct formulas), (3) the concept of relative velocity is still meaningful (but you will have to calculate it differently than the intuitive, galilean-relativity way of doing it), and (4) principle of inertia still holds (the motional state of an object does not change unless acted upon by an external force—but we may have to modify how that force relates to other kinematical quantities).
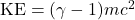Relativity changes most nonrelativistic formulas you have seen so far. Before, you were told kinetic energy is $\mathrm{KE}=\frac{1}{2}mv^2$ . Relativity tells you instead $\mathrm{KE}=(\gamma-1)mc^2$ . Before, you were told that momentum is 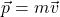$\vec p=m\vec v$ . Relativity tells you instead 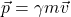$\vec p=\gamma m\vec v$ . Before, you could define force as 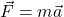$\vec F=m\vec a$ (provided that only a single force is acting on an object with constant mass m). Now, relativity says you must use the correct definition of force, 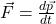$\vec F=\frac{d\vec p}{dt}$ , and the relationship between acceleration and force will no longer be so simple. (All symbols here defined the standard way.) With these relativistically correct formulas, the principles (such as of conservation of energy and momentum) apply as before.

Q2 – [OpenStax, Chapter 5, Question 20] We know that the velocity of an object with mass has an upper limit of c. Is there an upper limit on its momentum? Its energy? Explain your answer.

A2 – Upper limits in special relativity: There is no upper limit on momentum or energy of an object. In relativity, momentum is given by $\vec p=\gamma m\vec v$ and the total energy is given by $E=\gamma mc^2$ , with the Lorentz factor $\gamma = 1/\sqrt{1-v^2/c^2}$ . As speed v approaches c, the Lorentz factor increases without limit ( $\gamma \to \infty$ ), so both momentum and total energy can increase without an upper limit (which ought to be consistent with our intuition based on the conservation of energy and momentum).

Q3 – A charged pion ( $\pi^\pm$ ), an unstable particle of mass $140\ \mathrm{MeV/c^2}$ , is known to decay into a muon ( $\mu^\pm$ , mass $106\ \mathrm{MeV/c^2}$ ) and a neutrino ( $\nu_\mu$ ; we can treat it as massless here). In this decay of pion ( $\pi^\pm \to \mu^\pm + \nu_\mu$ ), typically only the muon is detected, the neutrino being an electrically neutral particle that rarely interact with other matter. Properties of neutrinos in this decay are inferred from measured properties of pion and muon. Explain, as conceptually as possible, why it is not possible for a pion to simply decay into a muon, without an associated neutrino. That is, why is this decay, $\pi^\pm \to \mu^\pm$ , impossible? (Note: If you happen to know about lepton numbers and neutrino flavors, please give an explanation that does not make use of concepts we have not yet covered.)

A3 – Single particle decay: The fact that single particle decay such as $\pi^\pm \to \mu^\pm$ is not possible can be argued from general principles in this way. Consider a pion at rest, possessing some amount of rest energy (in the form of mass). When it decays into a lighter particle, such as the muon, the total energy still needs to be conserved and the difference in the rest energies of the two particles have to go somewhere. If it is truly a single particle decay (i.e. no photon; no other particle), there is nothing else this energy can go into, and it cannot go into the muon, because giving muon kinetic energy necessarily means giving it some momentum. Conservation of momentum says that the total momentum should be zero, and with no other particle, the muon must have zero momentum in order to conserve momentum. So, conservation of energy and momentum prevents the pion from decaying into any other single particle, at least in its own reference frame.
Once we have established that $\pi^\pm \to \mu^\pm$ cannot happen in one inertial reference frame, it cannot happen in any other inertial reference frame, because principle of relativity says that laws of physics are all same in all inertial reference frames—so what is impossible in one inertial reference frame is also impossible in any other inertial reference frame.

Intro to Photons (questions and model answers)

Q1 – “Blackbody radiation” describes thermal radiation of electromagnetic waves (oscillating electric and magnetic fields emitted by an object at a temperature higher than 0 K). The attempts at explaining this phenomena is one of the first points (historically and conceptually) leading to the development of quantum mechanics. Give a brief description of theoretical attempts at explaining blackbody radiation, including the failed attempts based on classical mechanics and Planck’s successful description. Be sure to include following terms in your brief description: “ultraviolet catastrophe”, “Rayleigh-Jeans law”, and “Planck law”.

A1 – “Theoretical Description of Blackbody Radiation“: This is a model brief answer (given the emphasis on brief in the question, you may deduct points for answers that are overly long):
“With development of theory of electromagnetism and statistical mechanics (thermodynamics), physicists sought to explain electromagnetic radiation emitted by hot objects. One result of such attempts was Rayleigh-Jeans law, but while these theories agreed well with experimental observations of intensities at long wavelengths of emitted EM radiation, they did not agree at short wavelengths. While experimental observation showed that intensity decreased at very short wavelengths, Rayleigh-Jeans law predicted ever-increasing intensity at shorter and shorter wavelengths, a result now referred to as “ultraviolet catastrophe.” Max Planck was able to derive an expression that agreed with experimental observation (now called “Planck law”) by assuming that energies in thermal oscillators come in discrete packets of size hf, where h is now known as Planck’s constant, and f is the frequency of the oscillator.”
An answer that receives full credit could be shorter than this (if they don’t omit key information), but if it is much longer than above, it is probably overly long.

Q2 – [OpenStax, Chapter 6, Question 12] Suppose that in the photoelectric-effect experiment we make a plot of the detected current versus the applied potential difference. What information do we obtain from such a plot? Can we determine from it the value of Planck’s constant? Can we determine the work function of the metal? Explain how Planck’s constant and work function would be determined (if necessary, using equations).

A2 – “Analysis of Photoelectric Effect“: The plot described (detected current vs. applied potential difference) gives the information about the work function of the material, if the frequency of the light causing photoelectric effect is known. From consideration of energy conservation, $\mathrm{KE}_\mathrm{max}=hf-\phi$ , where φ is the work function of the material. The voltage applied which just barely stops current (“cutoff voltage”) gives the KE_max (voltage multiplied by electron charge), so the work function is the difference between photon energy (hf) and that maximum kinetic energy. If light sources of different frequencies are available, Planck’s constant can be measured also. You measure KE_max for a few different frequencies of light, and the slope of the resulting linear plot gives you the Planck’s constant.

Q3 – [OpenStax, Chapter 6, Question 14] Which aspects of the photoelectric effect cannot be explained by classical physics? Give at least 2 features which are not easily explained by wave model of electromagnetic radiation but are easily explained by the photon model of electromagnetic radiation.

A3 – “Quantum Mechanical Features of Photoelectric Effect“: Several features of the photoelectric effect are difficult to explain using the classical wave model of electromagnetic radiation. In the order of most difficult to least:

Dependence of features on intensity and frequency: The experiment shows that intensity of light is directly proportional to number of photoelectrons ejected, while the frequency of light is directly proportional to the maximum kinetic energy of photoelectrons ejected, and their effects are strictly separated this way. It is not easy to see in the wave model why this should be the case; in the photon model, with the interaction modeled as collision between photons of certain energy (given by frequency) and electrons in metal, this dependence is naturally understood.
Existence of “threshold frequency”: In the wave model, you should be able to compensate for lowered frequency by increasing the intensity of light, in order to give the electron a similar amount of “shaking,” or excitation, but experiments show this is not possible below a threshold frequency. In the photon model, this is easily explained as each individual photon not having enough energy to free the electron (and an electron in metal—which is in constant interaction with its surrounding—does not stay excited long enough to be struck by a second photon to gain energy from more than one photon).
Lack of a “measurable delay”: In the wave model, intensity of electromagnetic radiation is power per area. By limiting intensity, you limit the amount of power, or energy being transferred into the would-be photoelectron, so one could reason when intensity becomes low enough, a measurable amount of time needs to pass before the photoelectron gathers enough energy to be ejected (the estimate of time depends on what you use as the cross-sectional area for the electron). No such delay is measurable in experiment. In the photon model, even at the lowest intensity, each photon has the same energy, hf, they just come less frequently. So the first photon to strike an electron ejects the photoelectron, and no delay is expected.

The existence of threshold frequency is the biggest one (and any correct answer must contain it). One could come up with a clever argument to explain the next two (at least to some people), but there is no classical wave argument that explains why no amount of intensity will release photoelectrons below the threshold frequency.

Matter Waves and Semiclassical Models (questions and model answers)

Q1 – The images below show emission spectrum and absorption spectrum of the hydrogen atom, as an example. Explain, in general, why the patterns of bright emission spectral lines have an identical spectral position to the pattern of dark absorption spectral lines for a given gaseous element. Give one significant fact about how atoms interact with light which explains these features both on the emission spectrum and absorption spectrum.

A2 – “What Causes Spectral Lines“: Both the bright emission spectral lines and the dark absorption spectral lines are caused by discrete atomic energy levels. Electrons in an atom can only have energies in a countable number of energy levels (instead of being able to have a continuous spectrum of energy, like classical objects in a gravitational orbit). When an electron transitions from one energy level to another, it emits the difference in energy as a photon (if the electron is transitioning from higher energy level to a lower energy level) or it needs to absorb the difference in energy from a photon (in order to transition from a lower energy level to a higher energy level). Since these photons need to be of specific frequencies corresponding to the energy difference, both the emission spectrum and the absorption spectrum of an atom show discrete lines (bright for emission, dark for absorption) instead of a continuous range of frequencies.

Q2 – Answer following questions regarding de Broglie hypothesis of matter waves

[OpenStax, Chapter 6, Question 41] If an electron and a proton are traveling at the same speed, which one has the shorter de Broglie wavelength? Explain.
[OpenStax, Chapter 6, Question 42] If a particle is accelerating, how does this affect its de Broglie wavelength? Explain.
[OpenStax, Chapter 6, Question 43] Why is the wave-like nature of matter not easily observed in macroscopic objects?

A2 – “Matter Waves“: From de Broglie relationship λ=h/p,

If an electron and a proton have the same speed, the proton has the shorter wavelength, because its momentum is greater (greater mass for the same speed).
If a particle is accelerating (assuming “accelerating” means “speeding up” here), that means the magnitude of its momentum is increasing. As its momentum increases, the wavelength decreases, so the particle’s wavelength would decrease (but the wavelength is tied directly to the value of the momentum, not whether it is increasing or decreasing at the moment; two particles with exact same value of momentum would have the same wavelength at that moment in time, regardless of whether one is accelerating or not).
It is not easily observed because for most macroscopic objects, because the wavelength is unmeasurably short. A 1-kg object traveling at 1 m/s (momentum of 1 kg m/s) has wavelength less than 10^-33 m (an atomic nucleus is about 10^-14 m, for a sense of the scale).

Q3 – Explain: How is Bohr’s semi-classical model of hydrogen atom consistent with de Broglie hypothesis of matter waves?

A3 – “Bohr model and de Broglie relationship“: In the Bohr model, it is assumed that orbital angular momenta are quantized as $L=n\hbar(=nh/(2\pi))$ . You could “explain” this assumption, if instead you say (that is, you assume) that an electron could only orbit the atomic nucleus in such a way it forms a standing wave (that is, the circumference of the orbit is an integer multiple of wavelength of electron). (Note: In both cases, you are really entering an additional assumption that you cannot derive from classical mechanics. You can only “intuit” quantum mechanics from classical mechanics; you cannot derive quantum mechanics from classical mechanics, no more than you can “derive” an exact result from an approximation.)

Wave Mechanics Introduction (questions and model answers)

Q1 – [OpenStax, Chapter 7, Question 4] In wave mechanics, we use wave function $\Psi(x,t)$ to represent a particle. What is the physical meaning of the wave function $\Psi(x,t)$ ? [Note: If you cannot directly give a physically meaningful description of $\Psi(x,t)$ , feel free to describe instead a quantity related to $\Psi(x,t)$ that you can assign a physical meaning to.]

A1 – “Meaning of Ψ(x,t)“: The wavefunction $\Psi(x,t)$ is called “probability amplitude.” It does not have a physical meaning you could assign within classical mechanics (for contrast, amplitude of an electromagnetic wave is the maximum magnitude of electric field in the EM wave; or amplitude of a sound wave is the maximum displacement (or maximum change in pressure) of air molecules in the sound wave). It is not even clear what is the medium for this “probability wave,” in the context of classical mechanics. The physical meaning of $\Psi(x,t)$ is assigned through its absolute value squared, $|\Psi(x,t)|^2(=\Psi(x,t)^* \cdot\Psi(x,t))$ . $|\Psi(x,t)|^2$ is the probability density, meaning that the probability of detecting a particle in the interval from $x=x_0$ to $x=x_0+dx$ is given by $|\Psi(x_0,t)|^2\ dx$ . (We will get more into this, including calculations of expectation values using this idea, after Exam 2.)

Q2 – As strange as it may seem, the time-dependent Schroedinger equation, $-\frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} +V(x) \Psi(x) = i\hbar \frac{\partial \Psi}{\partial t}$ , is related to a concept that has been very familiar to you since Physics 4A. Identify what that familiar concept is and describe (conceptually, as much as possible) the mathematical mechanism used to guess at a wave equation which expresses that familiar concept.

A2 – “Origin of Schroedinger Equation“: The familiar concept is the idea of conservation of energy, or the idea that the total mechanical energy is kinetic energy plus potential energy: $\mathrm{TE}=\mathrm{KE}+\mathrm{PE}$ . The differential equation form of Schroedinger equation is simply this idea written out explicitly by use of momentum, energy, and position operators ( $\hat p=-i\hbar \frac{\partial}{\partial x}$ , $\hat E=i\hbar \frac{\partial}{\partial t}$ , and $\hat x=x$ ).

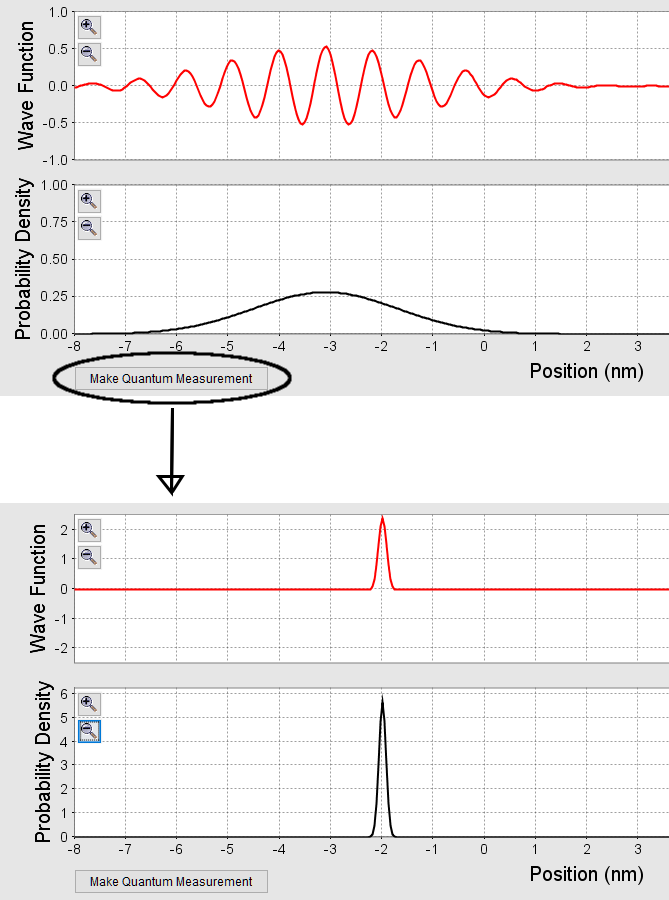
Q3 – [Note: This covers a topic you covered in PhET simulation lab [link to Lab: Quantum Mechanics Simulations].] Suppose you have a wave packet for a particle of mass m centered around position x = 0 m, with packet width of Δx = 10 μm. At time t = 0, you make a measurement of the particle’s position, and you measure it to be at x = 5.5 μm with a very high precision (let’s say Δx < 1 nm). If you immediately re-measure the particle’s position (that is, you make a second measurement also at t = 0 for all practical purposes), what will you measure as the particle’s position? Explain and/or justify your answer.

A3 – “Quantum Measurement“: The immediate second measurement yields a particle position consistent with the first measurement. That is, the second measurement will also yield x = 5.5 μm, give or take 1 nm (uncertainty of first measurement). This experimental fact is described as “wavefunction collapse” in the Copenhagen interpretation of quantum mechanics.

Note: What you saw in the PhET simulation is this. You start out with a wave packet of some width, as shown below(figure not in scale with numbers here). After a position measurement, the wave packet collapses into a very narrow width, and this collapsed wavefunction is now your new wavefunction, so any subsequent position measurement would yield position measurement consistent with the collapsed wavefunction, not the original wavefunction. To describe an additional feature that this question doesn’t ask about: in the simulation, you saw that this narrow wavefunction immediately spreads out; this is because of the high momentum uncertainty necessarily associated with this low position uncertainty state (from Heisenberg uncertainty principle, $\Delta x \Delta p \ge \hbar/2$ ). But this spreading out takes time, and that’s why it’s important that the second measurement be immediately after the first measurement, so that no time evolution of new wave state can take place.

Wave Mechanics Wrap-Up (questions and model answers)

Q1 – [OpenStax, Chapter 7, Question 2] Can the magnitude of a wave function (that is, $|\Psi(x,t)|^2=\Psi^*(x,t)\Psi(x,t)$ ) be a negative number? Explain why or why not.

A1 – “Positive-definite |Ψ(x,t)|²“: The magnitude of a wave function ( $|\Psi(x,t)|^2=\Psi^*(x,t)\Psi(x,t)$ ) cannot be a negative number. There are two ways to see it, one mathematical and one physical:
(1) Mathematical answer: For a complex number $z(=a+ib)$ , the product of its complex conjugate with itself is guaranteed to be a non-negative number, since, $z^*z=(a-ib)(a+ib)=a^2+b^2$ . Same holds for the complex-valued function, and the magnitude of a wave function is non-negative.
(2) Physical answer: the physical meaning assigned to $|\Psi|^2$ , that it represents probability density, requires it to be non-negative at all times everywhere, since negative probability is an unphysical idea. (Historical aside: Problem with negative probability density was what caused Schroedinger to abandon his first attempts at relativistic wave mechanics, settling for the non-relativistic equation which bears his name today.) Answer based on either approach alone can receive full credit.

Q2 – [Modified from OpenStax, Chapter 7, Question 8] Consider below two related, but slightly different questions.

Consider a localized free particle (also known as “wave packet”). Can we measure the energy of this particle with complete precision? If this is possible, give an example. If this is not possible, explain why not.
Consider a particle localized within a square well ( 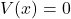$V(x)=0$ inside the well). Can we measure the energy of this particle with complete precision? If this is possible, give an example. If this is not possible, explain why not.

A2 – “Uncertainty Principle“:

No, it is not possible. Energy of the free particle is given by its kinetic energy, 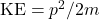$\mathrm{KE}=p^2/2m$ , and in order to localize a free particle, you must form the wave packet using traveling waves of different wavelengths, so that they constructively interfere at the location of the wave packet and destructive interfere everywhere else. This means this wave function has components of different magnitude of momentum ( 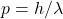$p=h/\lambda$ ), so it has components of different values of kinetic energy.
Yes, we can. Consider the example of infinite square well, when you take the particle’s energy eigenstate, for example, 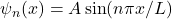$\psi_n(x)=A\sin⁡(n\pi x/L)$ . These energy eigenstates have a definite energy (that is, energy can be determined with complete precision), specifically 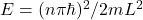$E=(n\pi \hbar)^2/2mL^2$ . This is still consistent with the uncertainty principle, because the uncertainty in momentum is not zero. 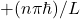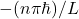This state allows two values of momentum, $+(n\pi \hbar)/L$ and $-(n\pi \hbar)/L$ , and these two values of momentum are associated with the resulting uncertainty in momentum.

Q3 – [OpenStax, Chapter 7, Question 11] If a quantum particle is in a stationary state, does it mean that it does not move? In what sense is a particle in a stationary state (a.k.a. energy eigenstate) “stationary”?

A3 – “Stationary State“: It doesn’t mean that it does not move (in fact, the whole concept of “motion” becomes difficult to address in quantum mechanics, where you can’t constantly measure the position of the particle to construct a trajectory). The best way to put it is, it becomes “stationary” in the sense that the stationary state (a.k.a. energy eigenstate) has a predictable time dependence, $\phi(t)=e^{-i\frac{E}{\hbar}t}$ , where E is the energy. This predictable time dependence cancels out when you measure physically meaningful quantities, such as $|Ψ|^2$ , and in fact, this is one quantity associated with a stationary state which does not change with time. So an energy eigenstate can be considered “stationary” in one sense that $|\Psi(x,t)|^2=|\psi(x)|^2$ (meaning that the probability density does not change with time).

Q4 – [OpenStax, Chapter 7, Question 16] For a quantum particle in a box, the first excited state ( $\Psi_2$ ) has zero value at the midpoint position in the box, so that the probability density of finding a particle at this point is exactly zero. Explain what is wrong with the following reasoning: “If the probability of finding a quantum particle at the midpoint is zero, the particle is never at this point, right? How does it come then that the particle can cross this point on its way from the left side to the right side of the box?”

A4 – “Nodes in Particle-In-a-Box“: This flawed reasoning is based on the classical misconception. The particle does not bounce around in the box—no more than classical wave on a string, set up as a standing wave, bounces around on the string (you wouldn’t argue “how does the wave get across the nodes on the standing wave,” once you understood superposition principle, right?). The fundamental misconception here is the underlying assumption that it is meaningful to talk about a position of the particle represented by the wavefunction. Until the particle is detected (by a position measurement), the particle does not have a definite position. Instead, the probability of finding the particle at a particular location is given by $|\Psi|^2$ . Once the particle is detected, then the wavefunction “collapses” (this is the Copenhagen interpretation) into a sharply peaked wavefunction around where the particle is detected (not the standing wave in the infinite square well), and this question becomes moot again.

Q5 – [OpenStax, Chapter 7, Question 18] Explain the connection between Planck’s hypothesis of energy quanta and the energies of the quantum harmonic oscillator. In what ways was Planck’s hypothesis (which led to Planck law of blackbody radiation) correct? In what ways was Planck’s hypothesis incorrect?

A5 – “Quantum SHO“: The energies of quantum SHO are given by $E_n=\hbar \omega(n+1/2)$ . So Planck’s assumption was right in the sense that the energy of the quantum-mechanical oscillator could only change by a unit of $\hbar\omega(=hf)$ . What Planck did not realize when he developed Planck law, however, was that there is a minimum energy a quantum SHO must have, $E_0=\hbar\omega/2$ , a.k.a. “zero-point energy”. This, however, did not affect Planck’s work, because he was mainly interested in exchange of energy between quantum SHO and electromagnetic waves (blackbody radiation).

Atomic Physics (questions and model answers)

Q1 – [OpenStax, Chapter 8, Question 1] Each possible state of hydrogen atom (more precisely, state of the electron in the hydrogen atom) can be uniquely identified with a set of quantum numbers, $n$ , $\ell$ , $m_\ell$ , and $m_s$ (these are the standard symbols for these four quantum numbers; your textbook uses $m$ in place of the unambiguous $m_\ell$ ). Identify the physical significance of each of these four quantum numbers.

A1 – “Physical Significance of Hydrogen Quantum Numbers“: Following are short descriptions of physical meanings of each quantum number, quantitatively and qualitatively:

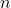$n$ (principal quantum number): indicates the orbital level (roughly, distance from proton) of the electron, and it is most closely associated with the energy levels (for hydrogen, $E_n=\frac{-13.6\ \mathrm{eV}}{n^2}$ ).
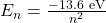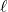$\ell$ (orbital angular momentum quantum number): gives the magnitude of orbital angular momentum of the electron, which is given by this formula: $L^2=\hbar^2[\ell\cdot(\ell+1)]$ .
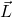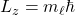$m_\ell$ (orbital angular momentum projection quantum number, or more commonly, magnetic quantum number): gives the projection of the orbital angular momentum ( $\vec L$ ) onto an axis (most commonly $z$ axis). The possible values are given by, $L_z=m_\ell \hbar$ . (The reason this is called “magnetic quantum number” is because in Zeeman effect, it’s this projection, along with the applied magnetic field, that determines the shifts in electron energy levels.)
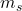$m_s$ (spin projection quantum number): gives projection of the spin angular momentum ( 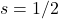$s=1/2$ and $S^2=\hbar^2[s\cdot(s+1)]$ since electron is a spin-1/2 particle) onto an axis (again, most commonly $z$ axis).

Q2 – [OpenStax, Chapter 8, Question 3] Compare and contrast the Bohr model of the hydrogen atom (that is, semiclassical model of H) and the Schroedinger model of the hydrogen atom (that is, fully quantum-mechanical model of H). Which parts of the fully quantum-mechanical model did Bohr get correctly? Which parts of the fully quantum-mechanical model does Bohr miss? (Hint: Look at the $n=1$ state. Aside from the prediction of energy levels, what else does the Bohr model predict which is not consistent with the Schroedinger model?)

A2 – “Comparison of Bohr Model with Schroedinger Model“: The semi-classical Bohr model gets two essential features of the fully quantum-mechanical Schroedinger model: (1) the energy levels (leading to the correct prediction $E_n \propto 1/n^2$ ) and (2) the fact that angular momentum is quantized (in the fully quantum-mechanical model, $L_z=m\hbar$ ). However, being a semi-classical analysis (that is, it is using classical mechanics, which is only an approximation of the real world, with a few parts replaced by quantum concepts), it does not hold up to close scrutiny. The most striking disagreement (with Schroedinger model and experiments) is the fact that the ground state of the hydrogen atom ( $n=1$ ) has zero angular momentum, not $L=\hbar$ as semi-classical orbits of electron in the Bohr model would have you believe (not to mention that electrons don’t actually move in orbits … but this falls more into interpretation of quantum mechanics, which is still an active area of research and not the best basis for invalidating the Bohr model).

Q3 – [OpenStax, Chapter 8, Question 4] Explain why spectral lines of the hydrogen atom are split by an applied external magnetic field. What determines the number and spacing of these lines?

A3 – “Spectral Lines under External Magnetic Field“: Splitting of spectral lines under an applied magnetic field is described by the Zeeman effect. To briefly summarize: The energy levels in hydrogen atom are degenerate, meaning that states corresponding to different quantum numbers $\ell$ and $m_\ell$ have the same energy ( $E_n=(-13.6\ \mathrm{eV})/n^2$ , no dependence on $\ell$ or $m_\ell$ ). But because these electric charges in orbit have a magnetic dipole moment (think of charges in orbit like a loop of current; magnetic dipole moment of a loop of current is given by $\mu=IA$ , where $I$ is the current and $A$ is the area of the loop), when you apply a magnetic field, the interaction of this magnetic dipole with the field results in the following change of energy (potential energy of magnetic dipole in a magnetic field): $\Delta E=-\vec \mu \cdot \vec B=-\mu_z B_z$ . The $z$ component of magnetic dipole moment is proportional to the $z$ component of orbital angular momentum (the constant of proportionality is called gyromagnetic ratio), which means $\Delta E \propto m\cdot B_z$ , and now the energy levels depend on the magnetic quantum number ( $m$ ). So, the magnetic quantum number determines the number of these lines (so, for example, for $n=2$ state, there are only 3 of these lines, because the two states with $m=0$ , one with $\ell=0$ and another with $\ell=1$ , still have the same energy). The spacing between the lines is determined by the applied magnetic field $B$ . (Technically, the spacing is determined by $B$ and the gyromagnetic ratio, but the orbital gyromagnetic ratio is a property of the electron and can’t be changed. $m$ does not play a role in determining the spacing because you are looking at states with adjacent values of $m$ , e.g. energy difference between $m=0$ and $m=\pm 1$ , not $m=2$ or $m=-2$ .)

Q4 – [OpenStax, Chapter 8, Question 9] List all the possible values of $s$ and $m_s$ for an electron. The spin of a particle is one of the identifying characteristic of a particle. Look up all possible values of $s$ and $m_s$ for the three other particles you know so far: photon, proton, and neutron. Comment on anything surprising you find.

A4 – “Spin Quantum Numbers“: The electron has spin value of $s=1/2$ (corresponding to the physical value $|\vec S|=\hbar \sqrt{s(s+1)}=\hbar\sqrt{3/4}$ ), and the possible values of $m_s$ are still given by the same rule that gives possible values of $m_\ell$ (that is, start at $-\ell$ and increase by 1 at a time until you reach $+\ell$ ), so the possible values of $m_s$ are $-1/2$ and $+1/2$ . The two other fermions you know (proton and neutron) has the same possible values of $s$ and $m_s$ ( $s=1/2$ and $m_s=\pm 1/2$ ). The photon exhibits an interesting exception. It is a spin-1 particle ( $s=1$ ), but its only possible spin projection values are $m_s=\pm 1$ (that is, $m_s=0$ is not a possible value for photon). The explanation for this must be found in relativistic quantum mechanics.

Q5 – [OpenStax, Chapter 8, Question 12] What is Pauli’s exclusion principle? Explain the importance of this principle for the understanding of atomic structure and molecular bonding.

A5 – “Pauli Exclusion Principle“: Pauli Exclusion Principle states: “No two indistinguishable fermions can have the same set of quantum numbers.” In the context of atomic physics, that means no two electrons can share the same set of quantum numbers $(n,\ell,m_\ell,m_s)$ in the atom. This is crucial in explaining the periodicity of multi-electron atoms (i.e. the periodic table), as you continue to add more electrons (for atoms with more protons than hydrogen), the electrons “fill up” the available states with different quantum numbers $(n,\ell,m_\ell,m_s)$ , starting with the lowest energies. This is why “valence shell” becomes an important idea to explain different possible chemical reactions (the energy change involved in shifting states of electrons in the outermost shell is less than pulling electrons out of the inner shell). Also, Pauli Exclusion Principle is a result of antisymmetrization requirement for fermions, and this requirement continues to play a role in explaining different molecular bonding (see: exchange force, or interaction).

Nuclear Physics (questions and model answers)

Q1 – [OpenStax, Chapter 10, Questions 1 and 2] (a) Define and make clear distinctions between the terms, neutron, nucleon, nucleus, and nuclide. (b) What are isotopes? Why do isotopes of the same atom share the same chemical properties?

A1 – Nuclear Terminologies:

Following four terms starting with “n” are distinct from each other and are not to be confused. In order: neutron is the charge-neutral version of proton. In fact, other than the fact that it has zero charge, it seems to behave very similar to proton (there are slight differences in mass; we think that is related to the fact that it has zero electrical charge, but in terms of strong and weak interactions, neutron is the same as proton). Because of this similarity, we use the term nucleon as an inclusive term that includes both protons and neutrons (the technical meaning of “nucleon” would be particles that are in atomic nucleus, which are protons and neutrons). Nucleus is the very dense part of the atom that contains nearly all the mass of the atom. It is made up of protons and neutrons. The term nuclide specifies the kind of atomic nucleus you are dealing with. A specific nuclide is specified by the number of protons and neutrons it contains (although technically these protons and neutrons can be arranged in different ways, any excited state of an atomic nucleus usually decays quickly into the ground state, which gives the nuclide properties that you can look up in a table).
We use the term isotope in the context of nuclear physics, and the word itself means “same place,” referring to the same place in the periodic table they occupy. It’s because different isotopes of an element (for example, carbon isotopes, of which two are stable, C-12 and C-13) have the same number of protons (same electric charge) and as a result exhibits nearly identical chemical properties. Outside of nuclear interactions, any difference between isotopes is attributed to the difference in mass (this can very slightly change the reduced mass and affect atomic energy levels), and since these mass-difference effects are very small, they are treated as being chemically identical. Different isotopes do engage in different nuclear interactions, since there neutrons get to play a role besides contributing to the mass.

Q2 – [OpenStax, Chapter 10, Question 4] Why is the number of neutrons greater than the number of protons in stable nuclei that have an atomic weight greater than about 40? Why is this effect more pronounced for the heaviest nuclei? And why are neutrons needed for stability of atomic nucleus in the first place?

A2 – “Stability of Atomic Nucleus“: When you look at the chart of nuclides, you notice a pattern for the stable nuclides, that they have about the equal number of neutrons as protons. At an intuitive/conceptual level, explanation for this would be the same explanation for why an atomic nucleus doesn’t blow itself apart with the Coulomb repulsion between the protons—there is a new, short-range strong nuclear force, which both protons and neutrons equally participate in. Additional neutrons help pull the nucleus together by exerting this strong nuclear force without the additional Coulomb repulsion. For heavier nuclei, two key things change: (1) energy of the interactions involved are larger (because there is a greater Coulomb repulsion to be overcome with the greater number of protons), and (2) with the larger nucleus, the average distance between interacting nucleons increase. At a conceptual/intuitive level, both things work to weaken the effective strong nuclear force. Since the strong nuclear force is a short-range force, a larger distance would make the force weaker, and larger interaction energy would mean we need to start accounting for relativistic nucleons, and this increases nuclear force needed to keep the nucleus together. So in order to overcome these effects, for heavier nuclei, more number of neutrons are needed to keep the nucleus stable.

Q3 – [OpenStax, Chapter 10, Questions 8 and 10] (a) Compare and contrast beta and alpha decays. What is the key difference and key similarity between beta ( $\beta^-$ and $\beta^+$ ) decay and alpha ( $\alpha$ ) decay? (b) What characteristics of radioactivity show it to be nuclear in origin and not atomic? Name at least two (but if you can, name three).

A3 – Alpha and Beta Decays

“Compare and contrast“: Both alpha and beta decays are parts of radioactivity. They are results of a change in nuclear energy level (unstable isotopes decaying into more stable, lower-energy isotopes), and both alpha and beta decays result in elemental transmutation (for example, beta decay of tritium results in the hydrogen turning into helium; alpha decay of uranium results in uranium turning into thorium). The key difference is in the particles being emitted in the decay. Beta decay results in ejection of an electron (or positron, for β+ decay), and alpha decay results in ejection of an alpha particle, a tightly bound state of two neutrons and two protons (also known as helium-4 nucleus). All other differences are tied to this key difference. In an alpha decay, having ejected a chunk of the nucleus, the atomic number goes down by 2 (lost 2 protons) and the mass number goes down by 4 (lost 4 nucleons). In a beta decay, since a neutron turns into a proton, the atomic number goes up one (gain 1 proton) and the mass number does not change (no net change in nucleon number). Alpha decay also tends to involve a larger change in nuclear energy. (And fundamentally, looking back from particle physics, being covered next week, we know beta decay involves the weak interaction and involves ejection of additional particles known as neutrinos, while alpha decay likely involves only the strong nuclear force, but these differences are not readily apparent when you are considering early nuclear physics only.)
“Nuclear Characteristics of Radioactivity“: Two biggest hints are (1) that there are new previously un-existing particles popping out, and (2) that the energy changes involved are large. Particularly for low-Z elements, the large energy involved makes it impossible for the observed phenomenon to be anything atomic. Atomic energy levels are on the order of 10 eV; radioactivity (such as beta decay of tritium) involves energy changes on the order of 10 keV or higher. Even for the high-Z elements, where electrons in inner shell could involve energy changes on the order of 10 keV (covered in Section 8.5, which we skipped), the additional particles (such as additional electrons) makes it impossible that radioactivity is atomic in origin (if one tries to make the argument that these were electrons somehow “trapped” in the atomic nucleus, then uncertainty principle considerations make this argument tenuous; the electrons were created in radioactivity, not merely released—here’s best link I could find in 5-minutes’ searching). There are additional evidences (some as a consequence of above two): (1) elemental transmutation (no atomic process changes elements), (2) emission of X-ray-like rays (gamma rays; but this is not the best evidence, as there are atomic processes that can emit X-rays, although nothing at the level of MeV range), and (3) application of electric and magnetic fields minimally affect radioactive decays; atomic processes are electromagnetic in nature.

Q4 – [OpenStax, Chapter 10, Question 14] Why does a chain reaction occur during a fission reaction? Describe and explain what conditions are necessary for the chain reaction.

A4 – “Chain Reaction“: Two key properties of fissile materials make chain reaction possible. (1) Being impacted by a neutron causes a fission reaction, splitting a heavy nucleus into two smaller nuclei, and (2) the fission reaction itself releases additional neutrons, which can impact another heavy nucleus and cause another fission reaction, releasing even more neutrons and causing even more fission reactions, which we call “chain reaction.” Whether this series of events can happen or not (and sustain it, once it occurs) is highly dependent on the isotope/nuclide. The nuclides for which self-sustained chain reaction take place are defined as “fissile” and highly controlled for nuclear nonproliferation reasons. For this chain reaction to be sustained, there needs to be a critical mass of fissile materials (for this reason, criticality is an important safety element for those working with nuclear reactors or weapons). When there is a critical mass of fissile materials, the additional neutrons released in fission reactions are likely enough to impact another fissile nucleus and continue on the fission chain reactions; when there is not a critical mass of fissile materials, the additional neutrons released in fission reactions are more likely to escape before impacting another fissile nucleus, resulting in few additional fission chain reactions.

Particle Physics (questions and model answers)

Q1 – [OpenStax, Chapter 11, Question 2] Distinguish fermions and bosons. In your answer, be sure to include/explain following terms and concepts: indistinguishability, exchange symmetry, particle spin, antisymmetric wavefunction.

A1 – “Fermions vs. Bosons“: As a matter of definition, fermions and bosons are distinguished by their spin. Fermions are half-integer spin particles (spin-1/2, like electrons, protons, and neutrons, or spin-3/2, like many heavy unstable baryons, or possibly spin-5/2 or higher for some atomic nuclei), and bosons are integer spin particles (spin-0, like pions and K mesons, spin-1, like photon, W boson and Z boson, and the gluon, or spin-2, like graviton; atomic nuclei with even number of nucleons also have integer spin). This classification has a fundamental importance in quantum mechanics because of the idea of indistinguishability: the subatomic particles are utterly indistinguishable, meaning there is no way to label one electron (or any other subatomic particle) apart from another. If two electrons in some quantum state were to be swapped, the resulting wavefunction, in some physically meaningful sense, have to be symmetric (the experimenter can’t know that they were swapped). This is called exchange symmetry (it’s a new kind of symmetry that has no counterpart in classical mechanics) and it must be obeyed whenever you have more than one indistinguishable (also “identical”) particles. For exchange symmetry to hold, the total wavefunction of the system can be either “even” (nothing changes) or “odd” (the overall sign reverses) on exchange of two indistinguishable particles. It is a theorem proven in relativistic quantum mechanics (see: spin-statistics theorem) that whether the total wavefunction is even or odd depends on the spin of the particle, and hence our reason for categorizing all particles as fermions (half-integer spin, obeying Fermi-Dirac statistics) or bosons (integer spin, obeying Bose-Einstein statistics). Fermion total wavefunctions are odd, or “antisymmetric” (because the sign reverses on particle exchange), and this is the reason behind the Pauli exclusion principle we covered in Chapter 8, Section 4.

Q2 – [OpenStax, Chapter 11, Questions 5 and 7] (a) What are six particle conservation laws listed in the textbook? Briefly describe them. (b) Why might the detection of particle interaction that violates an established particle conservation law be considered a good thing for a particle physicist (both experimental and theoretical)? (Note: Part (b) is an especially open-ended question; feel free to treat it as an essay prompt, but please do limit the length of your answer to not much more than a paragraph.)

A2 – Conservation Laws:

The six conservation laws listed in the textbook should be conservation of: (1) energy, (2) momentum, (3) angular momentum, (4) electric charge, (5) baryon number, and (6) lepton number. However, since strangeness is also listed in Section 11.2 (with the appropriate caveat that it is an approximate conservation law), it may be listed in addition to or in lieu of one of the quantities here (or conservation of energy and momentum may be combined as “conservation of 4-momentum,” in light of special relativity). The first four quantities (energy, momentum, angular momentum, and electric charge) ought to be familiar and what their conservation means (it means what it sounds like). Baryon number, lepton number, and strangeness require more explanation. These are new quantum numbers assigned to different particles, in order to explain why certain reactions (such as decay of a neutron into electron and positron, or decay of a proton into positron) are never seen. For example, protons and neutrons each carry baryon number 1 (and electrons and neutrinos carry baryon number 0), and electrons and neutrinos carry lepton number 1 (and baryon number 0). This would explain lack of the above-mentioned reactions. “Strangeness” is really better addressed in Question 4, so I’ll address it there; it ties into conservation of types of quarks and leptons, named “flavor“.
As mentioned in the question, this is an open-ended question. I’ll just mention some ideas that may be relevant (but there is no “correct” answer here; I am just explaining an attitude prevalent among physicists):
1. First, it is just darn interesting to see something new. That is probably why Niels Bohr suggested that energy and momentum might not be conserved in beta decays, because if true, that would open up exciting possibilities. It’s the same reason rubbernecking happens; it’s basic human psychology.
2. And beyond that, there are more selfish reasons. A new discovery in physics, such as neutrinos traveling faster than speed of light, would inspire more funding in physics research. It is difficult to apply for funding if all you can say is “we already know what we expect to see; we will see the same old phenomena all again in this new trillion-dollar facility” (so no one ever says that). Workers gather where there is work to be done, and new discovery (such as violation of an established law of physics) would make wonderful work for particle physicists.
3. And it would be a lucky thing even more so than a good thing. Not many scientists get to live in a time when their field is undergoing a paradigm shift. Maybe none of us would have been smart enough to figure out special relativity even if we had been born in 1879 like Albert Einstein, but one thing that’s for sure is, having born in the 20th century (or 21st century, for some of us), none of us will get the chance to be the one who formulated special relativity. Thomas Kuhn separates scientific work into normal science and revolutionary science. While most scientists console themselves with working within the frameworks of normal science, our true dream is in being part of a scientific revolution. (BTW, I don’t often quote so-called philosophers of science favorably; Thomas Kuhn, who holds a PhD in physics, is an exception.)

Q3 – [OpenStax, Chapter 11, Questions 8, 9, and 11] (a) What are the six known quarks? Summarize their properties. (b) What is the general quark composition of a baryon? Of a meson? Give the general rule for their quark composition and give two specific examples each, showing that these four total examples follow the rules given. (c) Why do baryons with the same quark composition sometimes differ in their rest mass energies?

A3 – Quarks

The six known quarks are up (u), down (d), charm (c), strange (s), top (t), and bottom (b) quarks. They are elementary fermions with spin 1/2. They are only known particles to carry fractional electric charges. Up, charm, and top quarks carry charge of +2/3 e, and down, strange, and bottom quarks carry charge of -1/3 e. They participate in all four fundamental interactions, gravity (they have mass and energy), electromagnetic (they carry charge, even if fractional), weak interaction (they—and all other known fermions—carry a “weak charge”), and strong interaction (quarks are the only known fermions to carry a color charge). The masses of quarks vary greatly. Up and down quarks have very small mass (the masses of protons and neutrons are basically relativistic effects), and the other quarks that make up unstable baryons and mesons have masses increasing in the order of discovery: strange quark, charm quark, bottom quark, and the top quark. Their measured masses are listed in the table by Particle Data Group.
Baryons consist of three quarks. For example, protons are made up of two up quarks and a down quark (uud), and neutrons are made up of one up quark and two down quarks (udd) (although especially in the case of protons and neutrons, it is more accurate to call this net quark content). The Omega baryon (the first step towards the quark model) is made up of three strange quarks. Mesons are made up of a quark and an antiquark. For example, a 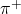$\pi^+$ meson is made up of an up quark and an anti-down quark. And neutral K meson ( 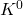$K^0$ ) is made up of a down quark and an anti-strange quark. The anti-neutral K meson ( 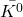$\bar{K^0}$ , yes, they are different) is made up of an anti-down quark and a strange quark.
Baryons with the same quark composition (for example, proton as compared to $\Delta^+$ ) have different rest masses because they have different energy. The best (simple) way to understand these is the higher-mass particle as an excited-state arrangement of the same quarks. Sometimes you can see the effect of these particles being in an excited state in their other properties (for example, $\Delta^+$ is a spin-3/2 particle); other times, you simply see these excited states decaying down to their lower-energy versions by emission of a photon or a meson like a pion which carries away no net quantity other than energy and momentum). When you look at the full table of baryons (and mesons), you see many resonances above the lowest-energy state listed. Those resonances are indicated with the same symbol (plus a number after them to indicate their rest energy) as the ground-state arrangement that has the same quark content. Knowledge of these resonances are as useful to particle and nuclear physics as knowledge of atomic levels is to atomic, molecular, and optical physics.

Q4 – [OpenStax, Chapter 11, Question 17] What is the Standard Model? Express your answer in terms of the four fundamental forces, 12 elementary fermions, force-mediator bosons (technically there are 12 of these, but no need to address their number), and one scalar (spin-0) boson (confirmed to exist in 2014).

A4 – The Standard Model (also known as Standard Model of Particle Physics, to distinguish from Standard Model of Cosmology or Standard Solar Model) is the most extensively tested model of interaction of elementary particles, including three of the four fundamental forces (electric forces unified with weak interaction in electroweak interaction and strong force described by quantum chromodynamics; the theory explicitly does not deal with gravity), by describing these forces as interaction mediated by force bosons (QED by photons, weak interaction by W and Z bosons, and strong interaction by bi-colored gluons) between elementary fermions, categorized into two sectors, leptons (does not participate in strong interaction) and quarks (carries color charge and participates in strong interaction). Leptons and quarks come in three generations each; each generation contains two fermions, with the weak interaction involving a W boson capable of changing one particle within the generation to the other particle (for example, electron couples to electron neutrino at the vertex involving a W boson, and an up quark couples to a down quark at the vertex involving a W boson). There are a total of 12 leptons and quarks, not counting their anti-particles separately (and it is still an unsettled research question whether neutrinos are their own antiparticle). The last piece of the Standard Model to be tested (and confirmed) is the Higgs mechanism (explaining electroweak unification), which was confirmed with the discovery of the Higgs boson at LHC. The Standard Model also includes features such as skewed generations (parameterized in CKM matrix for quarks and PMNS matrix for leptons). These are the features that describe the approximate conservation of lepton and quark flavors (of which “strangeness” is an example). Without skewed generations (that is, mismatch of energy eigenstates in strong interaction and weak interaction), the total “upness” and “downness” (described in isospin symmetry) would be conserved (a weak interaction would convert between up and down quarks but no other quarks), and the total “charmness” and “strangeness” would be conserved (a weak interaction would convert between charm and strange quarks but no other quarks). But because of skewed generations, a strange quark can turn into an up quark in a weak interaction, so strangeness is only approximately conserved (and there is no absolute conservation of total charmness and strangeness). Until recently, lepton flavor was thought to be conserved, but the discovery of neutrino oscillation put a stop to that idea (and hence the matrix to describe the generational mixing).

Now the joke here is, for a fundamental theory of elementary interaction between elementary particles, the Standard Model has a lot of parameters (19 parameters, which includes experimentally measured masses of elementary particles and mixing angles that describe skewed generations). For this and other reasons, no particle physicist considers the Standard Model to be the ultimate theory (you could call it “The Theory of Almost Everything“). What frustrates particle physicists today is that, despite more than a (literal) generation of research and efforts, we have found no better theory beyond the standard model (string theory has many bitter critics, who may at least be not “not even wrong“).

Coda

[ARCHIVAL NOTE: Below is the content of “Note on Peer Review” Canvas page]

The next Module item is your first peer-graded assignment, which covers conceptual questions from Chapter 1 topics. You will get the hang of these assignments as you complete the first few (and complete the peer reviews, which will give you some idea of what your peers will see, when they review your work).

To introduce peer-grading, below are videos from Spring 2018 Physics 4C class explaining the process.

There have been some key changes since, so let me re-record these overviews at one of the virtual class sessions this semester. Until the new recording is available, in summary, the changes are:

Instead of being assigned right at midnight, immediately after when the conceptual questions are due, the peer reviews will be assigned at 8 a.m. the following morning.
The grading rubric is changed to refer to completeness and effort, not correctness of answers.
Peer reviews are no longer anonymously assigned; you will see the names of reviewers and reviewees.