ARCHIVED – PHYS 4A Conceptual Questions

This is an archive of Physics 4A conceptual questions. The last semester these questions (and answers) were used was in Fall 2024 class, and with the recent re-organization of the course material, I don’t anticipate using them again, so this is a kind of “resting place” for this material.

General Instructions

[ARCHIVAL NOTE: Below are the general instructions used at the beginning of the conceptual questions set, under the “Instructions” heading]

This is a peer-graded assignment. After the assignment due date, you will be assigned 3 peer reviews for this assignment. Please follow the instructions in the peer review assignment (which also contains model answers and grading notes) to complete the peer reviews.

The conceptual questions below, some from the textbook and others that relate to the topics covered in the textbook, can mostly be answered adequately in one paragraph or so. If you see more than three questions, you only need to answer up to three questions for a complete submission.

Please answer the following three (3) conceptual questions in your response to this assignment. Use of text box for online submission is highly recommended.

[ARCHIVAL NOTE: Below are the general instructions used at the end of the conceptual questions set, immediately after the last question]

Please click on “Submit” button at the top of this page to submit your answers. Use of text box for online submission is highly recommended (text box has advanced editing options that can meet most needs). Use the file upload option if you have to upload images or PDF for your answers.

[ARCHIVAL NOTE: Below are the general instructions—under the “Instructions” heading—used at the beginning of the “peer review” assignment, which contained the model answers]

After the due date for [LINK to CONCEPTUAL QUESTIONS SET], you should have been assigned up to three classmates’ submissions for peer review. The links to these assignments are available within the page for [LINK to CONCEPTUAL QUESTIONS SET]; look for the links near the portion of the page showing your own submission info, either on the right side of the page or the bottom, depending on the size of your web browser window.

Please review the submissions using the provided rubric; mark the rubric based on the completeness and evidence of effort demonstrated. For a peer review to be considered complete, you must fill out the grading rubric, separately for each submission. I do encourage you to observe how your peers’ submissions compare to your own and leave an encouraging feedback. You can leave comments either within the rubric or outside of the rubric. Do please note that your peers cannot respond to you, as peer review communications only go one way, from the reviewer to the reviewee.

In case it’s helpful, below section provides model answers to the associated conceptual questions.

[ARCHIVAL NOTE: Below are the general instructions—as additional sections—used at the end of the “peer review” assignment]

Late Peer Reviews – There is some limited grace period between the peer review due date and when I assign peer review scores. Beyond this, please note there will be no extensions. Peer reviews must be received on time for them to be useful to the people you are reviewing. If you do not see any peer reviews assigned to you and it’s past peer review deadline, it’s because I removed all incomplete peer review assignments when I gave peer review credit.

“Mark as Done” – You must mark this assignment as done before you can move onto the next item in the Module. In this class, “mark as done” simply means you take responsibility for knowing the information on the page (whereas “view” requirement simply means your web browser accessed the information). So, if you feel you understood what is on this page and you take responsibility, please mark it as done, so that you can move on to the next page.

Rubrics

[ARCHIVAL NOTE: Below are “Conceptual Questions Rubric“, same rubric repeated for Questions 1, 2, and 3]

Conceptual Question 1: Completeness of the response to Conceptual Question 1 (or one of three questions answered)

2 pts – Complete: The response is clearly marked as a response to Conceptual Question 1 (or one of three questions answered) and demonstrates a good-faith effort at answering the question.
1 pts – Incomplete: The response is not clearly marked as responding to Conceptual Question 1 (or one of three questions answered) and/or good-faith effort at answering the question is not evident.
0 pts – No response: No response can be matched up to Conceptual Question 1 (or one of three questions answered).

[ARCHIVAL NOTE: Below is “Peer Review Rubric”]

Completeness: Completeness of peer reviews with evidence of effort.

3 pts – Complete: All three assigned peer reviews have been completed with a clear evidence of effort shown.
2 pts – Incomplete: One or more of peer reviews have not been completed, and/or lack of good-faith effort in the completed peer review(s) is evident.
0 pts – No reviews: None of the three assigned peer reviews have been completed in a meaningful way.

Kinematics (questions and model answers)

Q1 – Consider two rubber balls which are on two smooth tracks that begin and end at the same points but slope differently. The slope A slopes down first more steeply than the slope B, as shown in the figure. If the two balls are released at the same time: (i) How do the speeds of the balls when they reach the bottom compare? (ii) Which ball, if any, reaches the bottom first? Explain your answers, and assume that the balls stay on the track throughout their entire downhill roll.

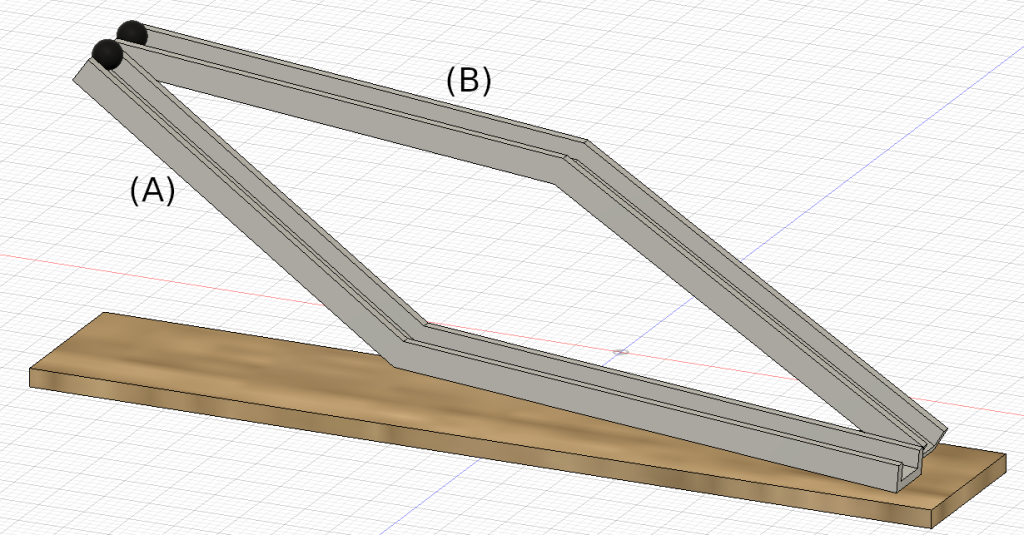
A1 – Comparison of two tracks: (i) The speeds of the two balls when they reach the bottom are the same. At this point in the course, it is O.K. to reach this answer intuitively without additional explanations/derivations. Later on in the course, we will be able to justify this answer based on energy conservation. (It is possible to give a justification using the v-squared kinematics formulas, but it’s not required for the answer to be considered correct.) (ii) The ball moving along track (A) reaches the bottom first. One of the ways to understand this result is to observe that, for track (A), the ball accelerates quickly first, allowing the ball to travel most of the track at a high speed, while for track (B) the ball accelerates slowly for about half the track, meaning the ball travels only the last segment of the track at a high speed. This makes the average speed of ball (A) higher, which means less time spent on the track (according to $\overline v = \Delta x / \Delta t$ ).

Below video recorded using Algodoo simulation software demonstrates this.

Also, this video on YouTube illustrates a similar idea with a physical demo: Gravitational Illusions. In this video, the track where the ball travels faster is actually longer.

Q2 – Consider each of the following scenario and explain whether or not the person/object described in the scenario is in free fall or not:

A tennis ball thrown straight upward, after it has left the hand: (i) on the way up, (ii) at the top of the motion, and (iii) on the way down.
A skydiver after having jumped out of an airplane, after they have reached the terminal velocity but before deploying the parachute.
An astronaut on the International Space Station performing an Extravehicular Activity while safely tethered to the station.

A2 – Free fall scenarios: Note that “free fall” means when only gravity acts on an object, and hence the object is accelerating at the gravitational acceleration.

The tennis ball is in “free fall” for (i), (ii), and (iii). Throughout the entire time after leaving the hand, the tennis ball is accelerating downward at 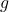$g$ . Note in particular that for (i), even while the ball is moving upward, it is considered to be in “free fall”, according to the definition of free fall.
At the terminal velocity, the skydiver is not in free fall. At the terminal velocity, the skydiver is moving at a constant speed (zero acceleration), because the net force due to gravity and air resistance is zero. Since forces other than gravity act significantly, this is not free fall.
The astronaut is in free fall (assuming the tether is not taut), because only gravity acts on the astronaut.

Q3 – The following video illustrates a demonstration known as “shoot the monkey”, in which a projectile in fired at a toy monkey. The projectile is aimed directly at the monkey, and the monkey is released into free fall at the moment the projectile is fired.

Consider this situation and describe 3 different ways in which you can modify the setup so that the projectile does not strike the monkey. At least 1 of the 3 ways must not change the aim or the timing of firing the projectile and releasing the monkey.

A3 – “Shoot the monkey”: There are several ways in which the projectile can be made to miss the monkey. Messing up the aim (aim the dart too high or too low) or the timing (fire the dart too early or too late) are some of the more obvious ways to miss the monkey. For the one method in which you are not allowed to mess up the aim or the timing, you can fire the dart very slowly. Specifically, if the dart travels so slowly that it does not hit the monkey before the monkey hits the ground, then the dart will not “reach the monkey in time” and miss the monkey. (Note, however, very fast dart will still hit the monkey, and even slow darts will be able to hit the monkey, as long as they are moving fast enough to reach the monkey before the monkey hits the ground.)

Newton’s Laws (questions and model answers)

Q1 – [OpenStax, Chapter 5, Question 2] Taking a frame attached to Earth (a portion of the ground) as inertial, which of the following objects cannot have inertial frames attached to them, and which are inertial reference frames? (a) A car moving at a constant velocity. (b) A car that is accelerating. (c) An elevator in free fall. (d) A space capsule orbiting Earth. (e) An elevator descending uniformly.

A1 – Inertial reference frames: Please take note: a part of taking a frame attached to Earth as inertial is treating gravitational force as a real force that need to be accounted for in Newton’s Second Law. Having said that, the objects which can be said to be used to define an inertial reference frame are (a) a car moving at a constant velocity and (e) an elevator descending uniformly. I can imagine some people being tempted to say that (c) an elevator in free fall and (d) a space capsule orbiting Earth should be inertial reference frames too, because you can see what looks like $\sum \vec{F}=0 \Leftrightarrow \vec{a}=0$ in these reference frames. But remember in both of these cases that gravitational force is acting on the objects in this frame. So the only way to apply Newton’s Law in these cases is to introduce pseudoforces (a.k.a. fictitious forces; read more about that in Section 5.6 Common Forces, subsection “Real Forces and Inertial Frames”) associated with the accelerating reference frame and use those pseudoforces to cancel out the gravitational force, making $\sum \vec{F}=0$ (as, e.g. an astronaut floats in the space capsule). We can make adjustments to accelerating reference frames to be able to use Newton’s Law within those frames. However, they aren’t inertial reference frames.

Q2 – [OpenStax, Chapter 5, Question 8] Which of the following statements is correct? For each statement, give a brief explanation why it is correct/incorrect. (a) Mass and weight are the same thing expressed in different units. (b) If an object has no weight, it must have no mass. (c) If the weight of an object varies, so must the mass. (d) Mass and inertia are different concepts. (e) Weight is always proportional to mass.

A2 – Mass vs. Weight: The starting point for the distinction is that mass is a property of the object, indicating how much stuff is in the object; “weight” is a synonym for “gravitational force” (more specifically, how much gravitational force is exerted on the object by the nearest astronomical body, such as a planet or a moon). The answer and explanation for each statement are below:

“Mass and weight are the same thing expressed in different units.”: False. For example, in SI units, kilogram (mass) and newton (weight) express fundamentally different things. You can see this care taken in Appendix B: Conversion Factors, where pound is not converted into kilograms, but instead into newtons (1 pound = 4.448 newtons). You can say that 1 kilogram of mass weighs 2.20 pounds (or 9.8 newtons, on Earth), but you cannot say that 1 kilogram is equal to 2.20 pounds (at least not in a physics class).
“If an object has no weight, it must have no mass.”: False. On Earth it would be true that an object with no weight also has no mass. But looking for counterexamples, we notice that weight is given by mass times gravitational acceleration ( 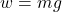$w=mg$ ) and instead of making 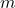$m$ equal to zero, we can make 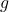$g$ equal to zero. If we were to take an object with nonzero mass very far away from any astronomical bodies, its weight (gravitational force on the object) will be zero, but its mass will remain nonzero.
“If the weight of an object varies, so must the mass.”: False. Similar as (b) above. As an example, on International Space Station, orbiting about 400 km above Earth, the weight of astronauts is about 89% of their weight on the surface of the Earth (take care not to confuse their weight, which does not go to zero, with their apparent weight, which does go to zero). But the masses of astronauts do not change as they go from the surface of the Earth onto the ISS.
“Mass and inertia are different concepts.”: False, mostly. Mass (i.e. how much stuff something has) determines inertia of the object (how much force do you need to apply in order to accelerate the object by some amount). In fact, in “weightless” environment, determining inertia of an object is how we measure its mass. The “mostly” adverb is used because mass is also used in different context in which inertia does not necessarily play a role: how much gravitational force is generated by the object? That is, mass serves as a “gravitational charge”. As far as we can tell by experiment, the “gravitational charge” of mass is same as its inertia (that is, mass of an object determined by measuring how much gravitational pull it produces, and mass of an object determined by how much it resists acceleration are the same), so for the moment, mass is the same as inertia.
“Weight is always proportional to mass.”: True. In fact, this is how spring scales and your bathroom scale work. Since 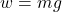$w=mg$ , when the mass doubles (keeping 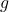$g$ constant), weight doubles too, and you can use this to calibrate a scale, given some constant 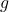$g$ . Now, what about the special case where 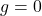$g=0$ ? We can still say that the weight is proportional to mass. When mass doubles, weight goes from 0 to 0, and we could say this is a kind of doubling, since $0 \cdot 2=0$ .

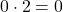Q3 – [OpenStax, Chapter 5, Question 11] Identify the action and reaction forces in the following situations: (a) Earth attracts the Moon, (b) a boy kicks a football, (c) a rocket accelerates upward, (d) a car accelerates forward, (e) a high jumper leaps, and (f) a bullet is shot from a gun.

A3 – Action and Reaction forces: We make sure that action/reaction force pairs follow the rule described in Chapter 5 Reading and Lectures (in particular, subsection “Newton’s Third Law”; and above all, make sure you are not describing a cause-and-effect relationship). Note in all these examples below, you can swap the “action” and “reaction” labels, and it will still be correct:

Earth attracts the Moon: the action force is the gravitational force due to the Earth pulling the Moon towards the Earth; the reaction force is the gravitational force due to the Moon pulling the Earth towards the Moon.
A boy kicks a football: the action force is the normal force from boy’s foot acting on the football, pushing the football forward; the reaction force is the normal force from the football acting on the boy’s foot, pushing the foot backward.
A rocket accelerates upward: the rocket accelerates upward by pushing on its fuel exhaust downward (action force); the downwardly-pushed fuel exhaust pushes back on the rocket upward (reaction force).
A car accelerates forward: the car accelerates forward by pushing on the road backward through friction force between its tires and the road (action force); the road pushes back on the tire forward through this same friction force (reaction force).
A high jumper leaps: there are several force pairs we can consider here (and they would all be correct, if they are correctly identified), but let’s consider the pair that most directly relates to the leaping motion. As the jumper pushes down on the ground through the normal force (action force), the ground pushes up on the jumper through the normal force (reaction force).
A bullet is shot from a gun: for the sake of simplicity, let’s say that the gun exerts force on the bullet (the truth is there is an expanding hot gas inside the gun barrel, which is what pushes on the bullet and the gun). The gun pushing forward on the bullet is the action force; the bullet pushing backward on the gun is the reaction force (a.k.a. “recoil”).

Free-Body Diagrams (questions and model answers)

[ARCHIVAL NOTE: This assignment has custom assignment instructions for the “Instructions” section, which is below]

The conceptual questions, that would have normally been below, are replaced by free-body diagram drawing exercises for this assignment. See instructions below.

Let’s do something different for this week’s “conceptual questions”. Instead of asking conceptual questions from the textbook, let’s practice drawing free-body diagrams for a variety of physical situations (situations taken from Chapter 5 and 6 of the textbook). The only way to make this a meaningful practice to have you draw many free-body diagrams (not 3, not 5, but 10 or more).

So, below are a number of situations, illustrated with a diagram and a short description. Please draw and submit free-body diagrams for the situations below. Choose 3 or more of the situations and clearly label your responses. There are free vector graphics software such as Inkscape you can use to draw the diagrams on a computer; you may also draw the diagrams on a piece of paper, take a photo or scan of the drawing, and upload it. Make sure your forces are clearly labeled.

[ARCHIVAL NOTE: And the peer review model answers are preceded by below notes]

Important Notes for Peer Review:

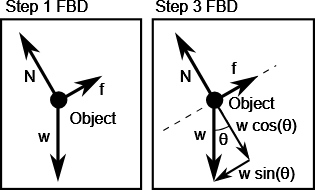
For each question below, I show two diagrams, one after the completion of Standard Strategy Step 1, and another after the completion of Standard Strategy Step 3 (with all the labels and decorations). The only thing that was required for this assignment was the one after the completion of Standard Strategy Step 1, so as you evaluate for completion and effort, please keep that in mind.
Assignment only requires completion and submission of 3 FBDs for full credit. While I hope many students made use of the opportunity for practice, additional FBDs beyond the three (3) required ones are not scored (do feel free to leave additional feedback that may be helpful).

Q1 – [From OpenStax, Chapter 5, Problem 63] Draw the FBD of the forces acting on the bird. Draw with enough detail to allow you to solve for the tension in the line.

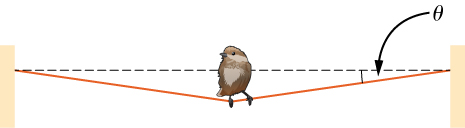
A1 – OpenStax Chapter 5, Problem 63:

Q2 – [From OpenStax, Chapter 5, Problem 66] Draw the FBD of the forces acting on the crate, if the crate is accelerating slightly up the frictionless slope.

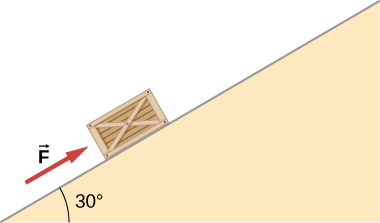
A2 – OpenStax Chapter 5, Problem 66:

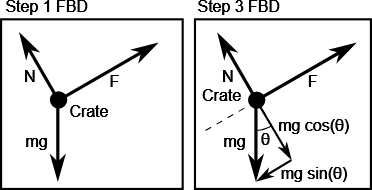
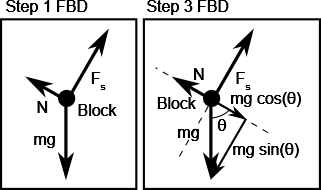
Q3 – [From OpenStax, Chapter 5, Problem 88] Draw the FBD of the forces acting on the block, if the block is resting on the frictionless ramp.

A3 – OpenStax Chapter 5, Problem 88:

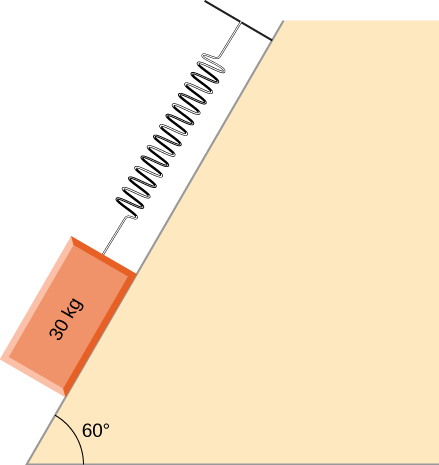
Q4 – [From OpenStax, Chapter 5, Problem 90] Draw the FBD of the forces acting on the block, if the block is accelerating slightly up the frictionless slope.

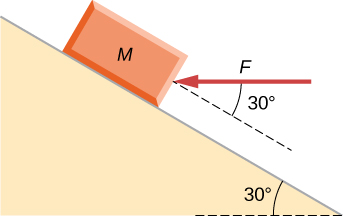
A4 – OpenStax Chapter 5, Problem 90:

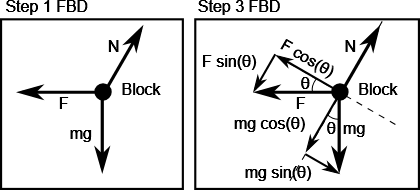
Q5 – [From OpenStax, Chapter 5, Problem 92] Draw the FBDs of the two blocks $m_1$ and $m_2$ . Assume $m_2$ is larger than $m_1$ .

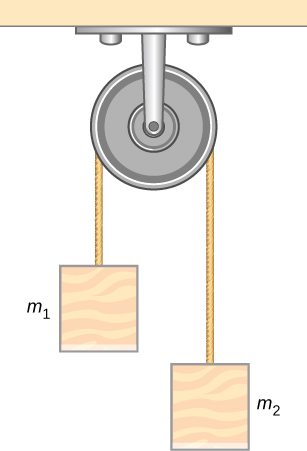
A5 – OpenStax Chapter 5, Problem 92:

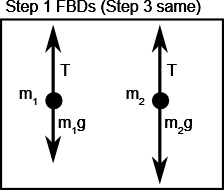
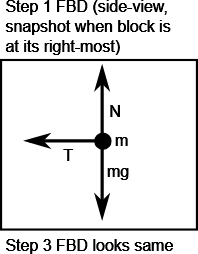
Q6 – [From OpenStax, Chapter 6, Question 15] Draw the FBD of the mass moving in the circular path shown. Choose and give description of a view which allows you to draw the clearest FBD.

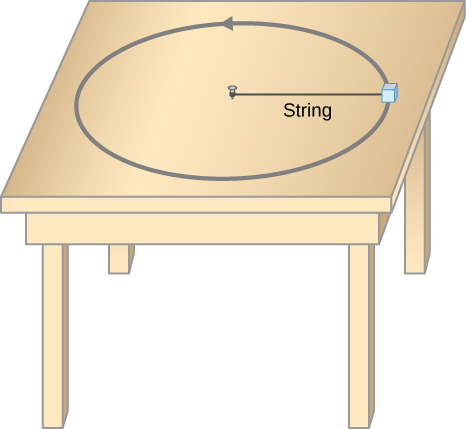
A6 – OpenStax Chapter 6, Question 15:

Q7 – [From OpenStax, Chapter 6, Problem 56] Below figure shows components of forces on an object resting on an incline without slipping. Draw the full FBD of the object, showing all the forces, not just components parallel to the incline.

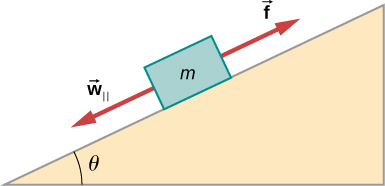
A7 – OpenStax Chapter 6, Problem 56:

Q8 – [From OpenStax, Chapter 6, Problem 73] If the roller coaster car is moving fast enough that the child feels pressed into the seat as the roller coaster passes point A, draw the FBD of the child, as the roller coaster goes through the point A.

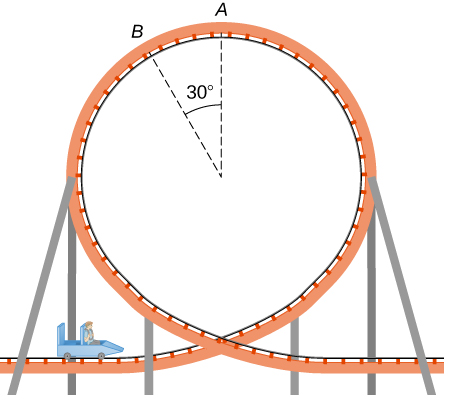
Q8 – OpenStax Chapter 6, Problem 73:

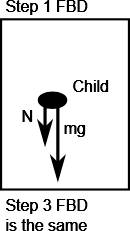
(And yes, at the top of the loop, the child is accelerating downward more than $g$ , and this acceleration should be consistent with the centripetal acceleration associated with the circular motion.)

Q9 – [From OpenStax, Chapter 6, Problem 108] Draw FBD of the block sliding slightly down the ramp. There is some friction between the ramp and the block.

A9 – OpenStax Chapter 6, Problem 108:

(The diagram is a bit busy, but yes, friction and $x$ component of $\vec F$ point in the same direction.)

Q10 – [From OpenStax, Chapter 6, Problem 123] Draw the FBDs of the two blocks shown, if there is a slight friction between each block and the horizontal surface.

A10 – OpenStax Chapter 6, Problem 123:

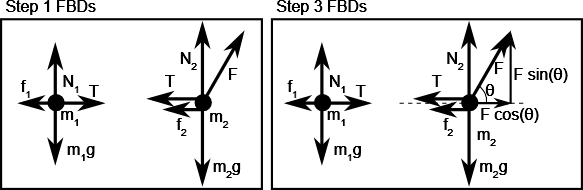
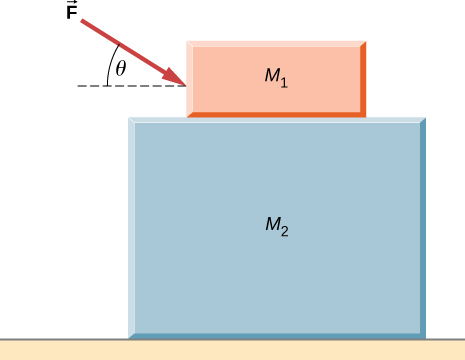
Q11 – [From OpenStax, Chapter 6, Problem 126] Draw the FBDs of the two blocks shown, if there is static friction between the two blocks, but the surface below $M_2$ is frictionless.

A11 – OpenStax Chapter 6, Problem 126:

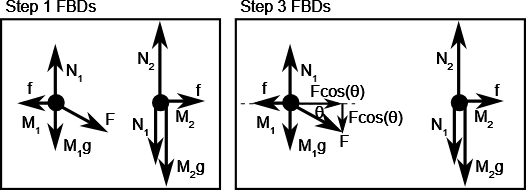
(Same letter labels indicate action/reaction force pairs; diagram not necessarily to scale; $N_2$ in particular needs to be a lot longer to be in scale.)

Conservation of Energy (questions and model answers)

Q1 – [OpenStax, Chapter 7, Question 1, slightly modified] Give three examples of something we think of as work in everyday circumstances that is not work in the scientific sense. For each example, answer: Is energy transferred or changed in form in your example? If so, explain how this is accomplished without doing work (or more precisely, explain where work in the scientific sense may be occurring that may not be immediately visible).

A1 – “Work not Work”: There are many possible examples; in the below three examples, I will try to address different meanings of the word “work” in everyday usage. For an answer to receive full credit, it does not necessarily have to cover these different meanings (three examples are requested in hope that some different meanings will be covered, but that hope is not enforced):

When an office-worker is “working” (e.g. sitting at a desk, possibly typing into a keyboard), no significant amount of mechanical work is done, because no macroscopic thing is being displaced while under a force. There is transfer of energy taking place (see basal metabolic rate), but it’s from a form of chemical energy (in chemicals in our body that provide energy necessary for our metabolism) to thermal energy (because we are warm-blooded animals). The interaction for this is happening at a microscopic level, so it needs a microscopic description, which we are not getting into.
After a weight-lifter lifts a weight, as they continue to hold the weight at the same height, no mechanical work is being done (no displacement), even though the weight-lifter will get tired and cannot hold that position indefinitely (so we think some work is being done). There is transfer of energy taking place (the usual metabolism; this activity might even be considered an exercise), but the (mechanical) work done occurs in the microscopic regime again.
A mathematician thinks very deeply about proving a difficult theorem while sitting still. This is a type of work (the mathematician is probably getting paid to do this), and although no visible movement takes place (so, no macroscopic mechanical work done again), there is a transfer of energy taking place, through chemical processes occurring in the mathematician’s brain. In fact, our brain is the largest single organ that uses energy in our body.

Oh, and of course, there is “working” in the sense of “operational, not broken.” If a door handle is “working” (or “works”), it just means all the connections are sound and it is able to be turned the way it should when a force is applied on it. Since this sense describes a state rather than a process, no transfer of energy takes place (for the simple reason that nothing is “taking place”).

Q2 – Give examples of: (a) two conservative forces, and (b) as many (but at least 3) non-conservative forces as you can think of. For each example of the conservative force, give the expression for the potential energy associated with the conservative force. For each example of a non-conservative force, give a situation where non-conservative force changes the total mechanical energy of a system.

A2 – Conservative forces vs. non-conservative forces:

There are only two conservative forces we will work with in this class: gravitational force and spring force. (Electric force and magnetic force are also good examples of conservative forces; we just won’t be seeing them much in this class.) For gravitational force, you will most often see its potential energy in this form, 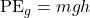$\mathrm{PE}_g=mgh$ , but later on, after we cover Newton’s law of universal gravitation, you will see the more general form. For spring force, the potential energy is given by 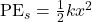$\mathrm{PE}_s=\frac{1}{2}kx^2$ , where $x$ is the displacement from equilibrium.
Following are forces you have seen in this class that are not conservative: (i) friction (both static and kinetic), (ii) air drag (a kind of friction force), (iii) normal force, (iv) tension force, (v) other applied force, etc. Basically, all forces not listed above are non-conservative forces and you can find examples where they change total energy of a system. Examples are easiest for kinetic friction and air drag, where they bring a moving object to a stop, dissipating away kinetic energy. For static friction, normal force, and tension force, think of a situation where these forces accelerate an object (e.g. static friction between tires and the road accelerates a car; normal force from upward-accelerating elevator floor accelerates you upward; tension force can be used to bring descending objects to a stop, etc.), which involves a change in kinetic energy, and since there is not a matching change in potential energy, these forces change the total mechanical energy of a system (same for any arbitrarily-specified applied force).

Q3 – [Adapted from Physics 10, also OpenStax, Chapter 8, Question 14] First, watch this video illustrating the situation given in Chapter 8, Question 14:

Answer the following questions: (a) What is the key difference that explains why the wrecking ball was able to break the window but not the professor’s chin? (b) In the second illustration (one that does not break the professor’s chin), find some evidence that the total mechanical energy of the ball decreased slightly. Describe this evidence, and explain why the total mechanical energy of the ball would decrease in this experiment.

A3 – “Professor risks his chin”: (a) The key difference is what the professor takes pains to describe: he has to be very careful in how he releases the wrecking ball; he wasn’t very careful as he pushed away the wrecking ball, before the ball came back and smashed the window. (b) If you watch the video carefully, you will see that the ball was touching the professor’s chin as it left, but on the way back, the ball doesn’t even reach his chin—it comes back to a slightly lower height than it left, and this represents a small loss of mechanical energy. And the culprit is the usual suspect: air resistance and other frictional forces (that we try hard to get rid of for idealized experiments but are never able to eliminate entirely, except possibly in the vacuum of space).

Collisions and Momentum Conservation (questions and model answers)

Q1 – [OpenStax, Chapter 9, Question 10] Can objects in a system have momentum while the total momentum of the system is zero? Explain your answer.

A1 – “Zero total momentum”: Yes, objects in a system with zero total momentum can individually have non-zero momentum. This is because momentum is a vector and direction matters. Just as the net force on a body can be zero while multiple non-zero forces act on the body (and they balance each other out), the net momentum (a.k.a. total momentum) can be zero while momentum of individual objects is not zero. Many examples exist, the most common one being a “stationary” sample of gas (gas molecules are whizzing around with non-zero momentum, but on net, the collection of gas molecules are not collectively moving in one direction). Other macroscopic situations can be found where two things are moving in opposite directions (or three or more things moving in a way that momentum vectors add up to zero). [Compare: if the total kinetic energy of a system is zero, there can be no (macroscopic) object in the system with non-zero kinetic energy.]

Q2 – [OpenStax, Chapter 9, Question 14] Describe an example of a system for which momentum is conserved but mechanical energy is not. Also give a reverse example: describe an example of a system for which kinetic energy is conserved but momentum is not (make sure your second example doesn’t involve kinetic energy turning into potential energy).

A2 – Conservation of momentum and energy:The key here is that two different conditions operate for conservation of momentum and conservation of (mechanical) energy. For conservation of momentum, the condition you need is, “no net impulse due to external forces” (so we watch out for external forces and see if they operate in such a way to impart a net impulse to our system). For conservation of mechanical energy, the condition you need is, “no net work due to nonconservative forces” (so we watch out for forces other than gravity or spring force doing net work).

Conservation of momentum but not mechanical energy: the completely (or “perfectly”) inelastic collision is the best known example. In a collision where two colliding bodies stick together, the total momentum of colliding bodies is conserved (no external forces). However, you can demonstrate algebraically (after solving the system with just conservation of momentum) that the total kinetic energy cannot be conserved in such a collision. We blame energy going into heat and sound, through friction and material deformation processes.
Conservation of kinetic energy but not momentum: Basically what we are looking for is a situation where velocity changes but speed does not change. Two common examples: (1) An object in a uniform circular motion (e.g. conical pendulum). Such an object has a changing momentum, but since its speed is not changing (“uniform” circular motion), its kinetic energy is conserved. (2) An object (e.g. a golf ball) undergoing a perfectly elastic collision with a very massive body, such as a wall. Looking at the system of just the object, the impulse imparted by the wall causes its momentum to change (and reverse direction of motion), but in the limit that the wall has infinite mass, negligible amount of kinetic energy is transferred to the wall, so the system of the object alone conserves kinetic energy.
In both examples, what operates is a net external force that either acts for long enough duration to impart a non-zero impulse (i.e. centripetal force in uniform circular motion) or the force is large enough that even with a short duration, a non-zero impulse is imparted (i.e. forces in collision).

Q3 – [OpenStax, Chapter 9, Question 17] Is it possible for the velocity of a rocket to be greater than the exhaust velocity of the gases it ejects? Explain: when this happens (oh, I guess this gives away some answer), the exhaust gas velocity and exhaust gas momentum are in the same direction as that of the rocket. How is the rocket still able to obtain thrust by ejecting the gases?

A3 – Rocket faster than exhaust velocity: Yes. While many examples can be found/thought about, the easiest one to cite would be the International Space Station. It is in orbit at a low-Earth orbit, with an orbital speed of 7.66 km/s. But the exhaust velocity of its maneuvering thrusters (any one of these examples that is not an ion thruster or an air-breathing engine) is less than 7.66 km/s. To understand this, consider the total momentum of the whole system of the spacecraft and the exhaust gas. If the exhaust gas is moving at any velocity “less” in the direction that the spacecraft is moving (this could include exhaust gas moving in the opposite direction), to conserve the total momentum, the spacecraft has more of momentum “more” in the direction that the spacecraft is moving. This is true even when the exhaust gas is still moving in the same direction as the spacecraft but at slower speed than the spacecraft (remember: initially the exhaust gas was moving with the spacecraft, at the same speed as the spacecraft).

Rotation (questions and model answers)

Q1 – [OpenStax, Chapter 11, Questions 3 and 4] Please answer following questions relating to rolling motion:

A wheel is released from the top on an incline. Is the wheel most likely to slip if the incline is steep or gently sloped?
Which rolls down an inclined plane faster, a hollow cylinder or a solid sphere? Both have the same mass and radius.

A1 – Rolling motion: There are usually two ways to approach rolling motion; one is through using conservation of energy approach (analyze the situation by considering kinetic energy in two parts, translational kinetic energy and rotational kinetic energy), and another is through consideration of torques produced by forces. The first question (a) is best approached through consideration of torques, and the second question (b) is best approached through conservation of energy.

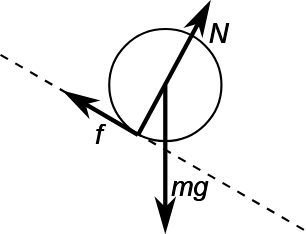
The free-body diagram above shows forces acting on a wheel rolling down an incline (incline shown in dotted line; forces shown with solid arrows, tail being placed at the location where the force acts). As you look at the FBD, the first thing you should see is that, about the center of mass of the wheel, neither the normal force nor the gravitational force generates a torque. The only force that generates a torque about the center of mass is the friction force (static friction force, when the wheel rolls without slipping). The normal force depends on angle $\theta$ the incline makes with horizontal as 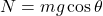$N=mg\cos⁡\theta$ , and since the maximum possible value of static friction force is proportional to 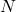$N$ , increasing 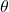$\theta$ reduces the maximum possible value of static friction force and makes it more likely that the wheel will slip (in addition, steeper incline will also be connected with larger value of acceleration and angular acceleration, if the wheel is to roll without slipping).
Whichever object has smaller rotational inertia will roll down the incline faster, since smaller fraction of the energy needs to go into rotational kinetic energy ( 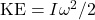$\mathrm{KE}=I\omega^2/2$ ) in order to keep the object rolling without slipping. A hollow cylinder has more mass farther out from the center of mass (all the masses at radius 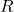$R$ of the cylinder from the longitudinal axis going through center of mass), so it has a larger rotational inertia than a solid sphere, so a solid sphere will roll down the inclined plane faster.

Q2 – [OpenStax, Chapter 11, Question 11] What is the purpose of the small propeller at the back of a helicopter [known as tail rotor] that rotates in the plane perpendicular to the large propeller [known as main rotor]?

A2 – Helicopter rotors: The purpose of the tail rotor is to keep the helicopter from spinning out of control. As the helicopter spins up (or slows down) the main rotor, it is applying a torque on the main rotor. By Newton’s Third Law (well, the rotational version of it), this means there will be a reaction torque on the helicopter, which will tend to spin the helicopter in the opposite direction to the main rotor (you can also look at this in terms of conservation of angular momentum). So, to keep the helicopter stable, there needs to be a mechanism to apply additional torque on the helicopter, in order to balance the counter-torque from the main rotor, and for the helicopters that have the tail rotor, the main purpose of that tail rotor is to provide this additional torque that can be used to balance the counter-torque. (There are other helicopter designs—especially common with quadcopter drones you might have seen—which use large rotors that rotate in opposite directions (2 or more main rotors) in order to balance the body of the helicopter; you can recognize these with multiple large rotors and no tail rotor.)

Q3 – [Adapted from Physics 10 Chapter 7 essay assignment] Precession uniquely illustrates features of rigid-body dynamics that requires vector properties of angular momentum and torque for clear explanation. The following video illustrates precession (click on the link to watch it on YouTube): MIT Physics Demo — Bicycle Wheel Gyroscope
Please answer the following conceptual question:
The motion you see in the video above, the slow, horizontal rotation of a spinning bicycle wheel with its axis oriented horizontally, is called “precession,” and we can talk about “rate of precession,” in terms of how quickly the bicycle wheel rotates horizontally. In the above video, the bicycle wheel precesses once about every 5 seconds. Make a prediction and explain your prediction: if you spun up the bicycle wheel to spin faster before you let go of one end, will the bicycle wheel precess faster or slower? (Or, another way to answer the same question is, if you spun up the bicycle wheel to spin slower before you let go of one end, will the bicycle wheel precess slower or faster?)
One resource that may help you gain an understanding of this phenomenon:

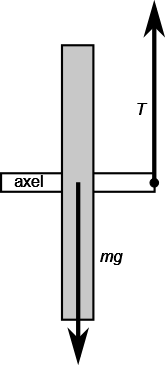
A3 – Precession: If the wheel is spinning faster, it will precess slower. What causes precession is the torque due to gravitational force. In the diagram shown on the right [below], you can see that the gravitational force causes a counter-clockwise torque about the right end of the wheel axel being supported with string, or using the cross-product, you can say that the gravitational force generates a torque which points out of the page. Torque is related to angular momentum in the same way force is related to momentum: $\tau=\Delta L/\Delta t$ . So this torque due to gravitational force causes the wheel’s angular momentum to change, and when the wheel has a pre-existing angular momentum (it’s spinning), this change of angular momentum causes the orientation of the axel to change, resulting in the precession motion. Below diagram illustrates how these changes in angular momentum $\Delta \vec L$ add up to the angular momentum $\vec L_0$ “going around a circle” and ending up at the same position, which is the description of precession. When the initial angular momentum $\vec L_0$ is large, this “circle” (like any vector that isn’t literally representative of displacement, this geometric language is an analogy) has a larger “radius”, with a matching larger “circumference”, so it makes more lengths of $\Delta \vec L$ to make one full circle (the torque due to gravitational force does not change), so a faster spin rate (larger initial angular momentum) leads to a slower precession rate.

Newton’s Law of Universal Gravitation (questions and model answers)

Q1 – [OpenStax, Chapter 13, Question 4, with modifications] Please answer following questions relating to orbital motions.

Describe what a “bound orbit” and an “unbound orbit” are. What are the key distinctions between them?
It is said that a satellite with negative total energy is in a bound orbit, whereas one with zero or positive total energy is in an unbounded orbit. Explain why and describe the convention for gravitational potential energy which makes this true.

A1 – Orbital motions: Newton’s Law of Universal Gravitation is the last piece of mechanics we needed in order to discuss orbital motions in full, so that we can deal with gravitational force which varies as $1/r^2$ (and potential energy which varies as $1/r$ ).

The terms bound orbit and unbound orbit have meanings that you would have guessed based on the meaning of the English word “bound” (past participle of “bind”). To make it more specific/technical, a bound orbit is an orbit in which the orbiting body remains within a finite distance from a center of the orbit. A bound orbit can be very complicated when more than 2 bodies are interacting, and the distance between the bodies can vary much throughout the orbit, but there is a finite maximum separation distance between the bodies. An unbound orbit is an orbit (“open orbit”) in which the “orbiting” object can/will get infinitely far away from the center of the orbit (the scare quotes around “orbiting”, because an object on unbound orbit will have a closest approach once and go away into infinity, never to be seen again). The one key distinction between these two types of orbits is the existence of a finite maximum separation distance. For a bound orbit, you can estimate this maximum separation distance based on conservation of mechanical energy. For an unbound orbit, you would estimate, based on conservation of mechanical energy, that the orbiting body can get infinitely far away.
In the context of satellite motion, we use the “universal reference point” of setting 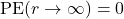$\mathrm{PE}(r \rightarrow \infty)=0$ , so that the interaction potential energy of two objects infinitely far away from each other is zero. This makes the potential energy for finite distance $r$ negative for attractive interactions (and positive for repulsive interactions). You can quickly estimate whether a given satellite is in a bound orbit by looking at its mechanical energy. 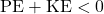If it has a negative mechanical energy ( $\mathrm{PE}+\mathrm{KE} < 0$ , meaning the kinetic energy is not as positive as potential energy is negative), then even at the maximum possible distance away (where you might have 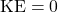$\mathrm{KE}=0$ ), it has a non-zero potential energy, meaning that the maximum separation distance is a finite number (i.e. a bound orbit). If it has a positive mechanical energy, then the satellite is in an unbound orbit, as it has enough kinetic energy to get out of the potential well (let $r \rightarrow \infty$ ) and still be moving. This way of tying total mechanical energy to bound/unbound orbit depends on using the universal reference point described above. 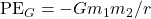Formulas such as $\mathrm{PE}_G=-G m_1 m_2/r$ derived and used in this class uses this universal reference point convention.

Q2 – [OpenStax, Chapter 13, Question 7] Some satellites are placed in geosynchronous orbits. Describe what is special about these orbits (in particular, describe if there are any restrictions on over what ground coordinates geosynchronous satellites can be placed) and answer the minimum number of satellites required, if these satellites are being used for a global communication network, allowing for real-time communication between any two points on Earth.

A2 – Geosynchronous orbits: Geosynchronous orbits are what they sound like—they are synchronous with “geo” (Earth). More specifically, satellites in geosynchronous orbits are directly above a single spot (latitude and longitude) of Earth throughout their orbit. So they should have a period of 24 hours (to match period of Earth’s rotation), and they can only be placed directly above equator of Earth (you can place satellites elsewhere with a period of 24 hours, but they won’t technically be geosynchronous, because their latitude will be changing throughout their orbit—hm, Wikipedia distinguishes geostationary orbit with geosynchronous orbit; we will be using the term loosely in this class, whether you use “geosynchronous” as being synonymous with “geostationary” won’t affect what answers are considered correct). For communication satellites in geostationary orbit, you need 3 for global coverage. Although with 2 satellites you will have a line-of-sight contact with every point on the Earth from one of the two satellites, the satellites won’t have line-of-sight contact with each other, making communication from one hemisphere of Earth to the other side not possible. With 3 satellites, you can place them in such a way that each satellite has line-of-sight contact with the other two satellites and every point on the Earth has a direct line-of-sight contact with at least one satellite.

Q3 – [OpenStax, Chapter 13, Question 9] The diagram below shows an elliptical orbit of a satellite ( $m$ ) about a much larger mass ( $M$ ). Please answer following questions:

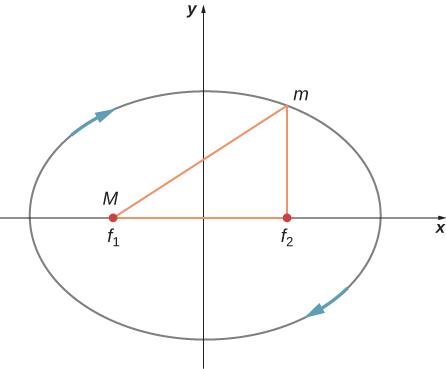
At which point in the orbit is the satellite’s speed greatest? Least?
Which conservation law (or laws) determines that the speed of the satellite at these points is greatest/least? Give a brief explanation.
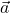Describe the relative direction between these three vector quantities at these points (where the speed is greatest/least) and give a brief statement regarding physical significance of these relative directions: force ( $\vec F$ ), acceleration ( $\vec a$ ), and velocity ( $\vec v$ ).

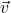A3 – Elliptical orbit:

The orbital speed of the satellite is the greatest at the point nearest mass 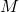$M$ , which is the left edge of the ellipse in the figure above (“perihelion”). The orbital speed of the satellite is the least at the point farthest mass M, which is the right edge of the ellipse (“aphelion”).
These speeds can be determined from conservation of energy. If the speed and distance of the satellite 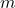$m$ is known at one point in the orbit, from conservation of energy, the total energy, 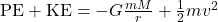$\mathrm{PE}+\mathrm{KE}=-G \frac{m M}{r}+\frac{1}{2}m v^2$ , must remain constant, which gives orbital speed $v$ as a function of distance $r$ . At shorter distance $r$ , the gravitational potential energy becomes more negative, which means speed $v$ must be greater to keep the total energy constant.
In addition to conservation of energy, conservation of angular momentum also operates in determining that the satellite moves faster at perihelion than aphelion. As the rotational inertia of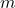 $m$ varies with 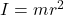$r$ ( $I=mr^2$ for point mass), and angular momentum is conserved in 2-body orbital motion (gravitational force does not produce any torque, because it is a central force), at shorter distance $r$ , the angular velocity $\omega$ should be greater to keep angular momentum constant (and $\omega$ is greater by enough amount that the tangential velocity, $v_t=r\omega$ , at perihelion is greater than aphelion). These two conservation laws give results that are consistent with each other (… thankfully, because we technically have an overdefined system here).
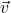At the perihelion and the aphelion, the force ( $\vec F$ ) and the velocity ( $\vec v$ ) are in perpendicular directions. Since acceleration ( 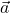$\vec a$ ) is always in the direction of the net force, this means that the acceleration is in a perpendicular direction to velocity, so it’s only acting to change the direction of velocity, not the magnitude. So, at the perihelion and the aphelion, the orbital speed is not changing (… consistent with the fact that at these points, the speed is at an extremum). Please note that these relationships hold only at the perihelion and the aphelion. At other points in the elliptical orbit, some component of force (and hence acceleration, 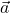$\vec a$ ) is parallel to velocity 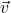$\vec v$ , resulting in change in speed.

Simple Harmonic Motion (questions and model answers)

Q1 – [OpenStax, Chapter 15, Questions 1 and 2] Please answer following questions relating to simple harmonic motion (SHM).

What conditions must be met to produce SHM?
If frequency is not constant for some oscillation, can the oscillation be SHM?
Please give an example of an oscillatory motion where the frequency of oscillation may depend on the amplitude.

A1 – Conditions for Simple Harmonic Motion (SHM): SHM is characterized as motion occurring under a Hooke’s Law type restoring force ( $\vec F=-k \vec x$ ). It can also be associated with a potential energy that takes a quadratic form, as a function of displacement from equilibrium (i.e. $U \propto x^2$ ).

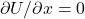While we could simply say that, for SHM to occur, the object must follow a potential energy function of the form $U=\frac{1}{2}k x^2$ , it’s worth parsing out some distinct features: (1) There must be an equilibrium (that is, point where $\partial U/\partial x=0$ , so the net (conservative) force on the object is zero at the point). (2) This equilibrium must be stable, meaning 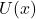$U(x)$ is concave up at this equilibrium, so that at points away from the equilibrium, the slope of 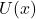$U(x)$ slopes towards back to equilibrium, which results in a restoring force pushing objects back to equilibrium. (3) The restoring force should increase linearly with displacement (with the help of Taylor polynomials, you can see that this is a requirement at least approximately met by most potential energy functions 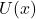$U(x)$ meeting conditions (1) and (2)).
No. By definition (or derivation from the equation of motion, 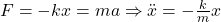$F=-k x = m a \Rightarrow \ddot x = -\frac{k}{m} x$ ), SHM is a type of oscillatory motion to which we can fix a constant frequency of oscillation. An arbitrary oscillation may be described as a superposition of multiple SHM, with “harmonics”. We might also have oscillatory motions for which the natural frequency of oscillation is a function of amplitude—at a fixed amplitude, this might be described similarly as SHM, but this is also not a SHM.
The one example given in the textbook is pendulum motion. For small amplitudes, it may be approximated as a SHM, but for arbitrarily large amplitudes, it is not a SHM, as the frequency of oscillation depends on the amplitude. Also, we can consider oscillation of a ball moving back and forth in a round-bottom (maybe semi-spherical) bowl. For small amplitudes it may be approximated as a SHM, but for large amplitudes, it is not a SHM.

Q2 – [OpenStax, Chapter 15, Question 12] Pendulum clocks are made to run at the correct rate by adjusting the pendulum’s length. Suppose you move from one city to another where the acceleration due to gravity is slightly greater, taking your pendulum clock with you. Will you have to length or shorten the pendulum to keep the correct time, other factors remaining constant? Explain your answer.

A2 – Pendulum frequency: As derived in Section 15.4, for small amplitudes, the natural frequency of simple pendulum oscillation is $\omega = \sqrt{g/l}$ , where $l$ is the length of the simple pendulum. Where the pendulum was calibrated, $\omega$ was set to give the correct time. When the pendulum is moved where the local value of $g$ is higher, in order to keep the value of $\omega$ the same, we would have to make $l$ higher, so that the ratio $g/l$ does not change.

Q3 – [OpenStax, Chapter 15, Question 14] With the use of a phase shift, the position of an object may be modeled as a cosine or sine function (as a function of time). If given the option, which function would you choose (Note: this is an open-ended question; there is no wrong answer; just be sure to explain your choice)? Assuming zero phase shift, if you are using a sine function to model the position of an object, what are the initial conditions of the oscillator—that is, the initial position, velocity, and acceleration of the oscillator at $t=0$ ? How about if you use a cosine function to model the position?

A3 – Mathematical description of oscillation: While recognizing that many students may prefer sine (and you can give many good reasons for that), I will say that I myself prefer cosine. That is, the default way I would write down an oscillatory motion is as $x(t)=A \cos⁡(\omega t+\phi)$ . You may also begin to see this tendency in your textbooks. The biggest reason for this is mathematical. As you will soon (maybe in a year?) see, it is mathematically very convenient to use complex exponentials to describe oscillatory phenomena. That is, use $\tilde x(t)=A e^{i(\omega t+\phi)}$ , instead of trigonometric functions. In this representation, the real component is $A \cos⁡(\omega t+\phi)$ and the imaginary component is $i A \sin⁡(\omega t+\phi)$ , so it is convenient to associate the real component with the default representation of oscillatory motion. A second reason I might cite for this preference is the common way lecture and lab demos are set up. It’s easier to start a SHM in a way $x(t)$ is described by $A \cos⁡(\omega t)$ (that is, with $\phi=0$ ), as you will see in the second part of the answer.
The second part: if we describe the SHM as $x(t)=A \sin⁡(\omega t)$ , this is what you will see. At $t=0$ , you have $x(t=0)=0$ . Since this is equilibrium position, this also means $a(t=0)=0$ . For the velocity, we have to take a derivative. $v(t)=x'(t)=A \omega \cos⁡(\omega t)$ , so at $t=0$ , you have $v(t=0)=A \omega$ . So the sine function representation of SHM describes a SHM which starts out at equilibrium with some non-zero initial velocity.
If we describe the SHM as $x(t)=A \cos⁡(\omega t)$ , at $t=0$ , you have $x(t=0)=A$ (SHM is at the amplitude of oscillation, the maximum displacement). Taking the first derivative, $v(t)=x′(t)=-A \omega \sin⁡(\omega t)$ , and at $t=0$ , $v(t=0)=0$ . For the acceleration, we take one more derivative: $a(t)=v′(T)=-A \omega^2 \cos⁡(\omega t)$ , so at $t=0$ , $a(t=0)=-A \omega^2$ (the acceleration causes the SHM to accelerate back towards the equilibrium).
Both descriptions are equally valid. Just be sure to keep track of the initial conditions that apply and their physical significance.

Waves and Sound (questions and model answers)

Q1 – [OpenStax, Chapter 16, Question 27] Many of the topics discussed in this chapter are useful beyond the topics of mechanical waves. It is hard to conceive of a mechanical wave with sharp corners, but you could encounter such a wave form in your digital electronics class, as shown below. This could be a signal from a device known as an analog to digital converter, in which a continuous voltage signal is converted into a discrete signal or a digital recording of sound. What is the result of the superposition of the two signals?

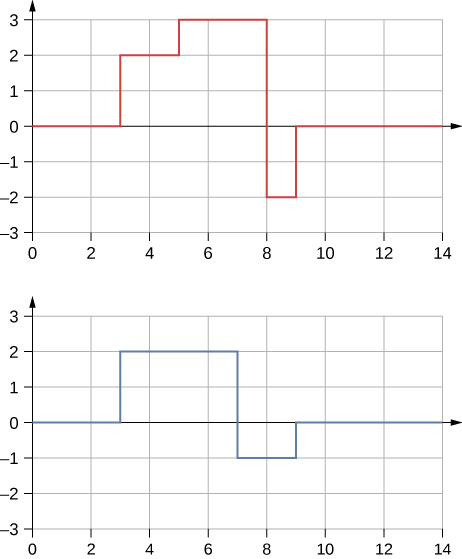
I encourage you to give your answer in graph form (hand-drawn, or using a free tool such as GeoGebra), but all else failing, you may also give your answer in words, describing the resulting piecewise linear function shape.

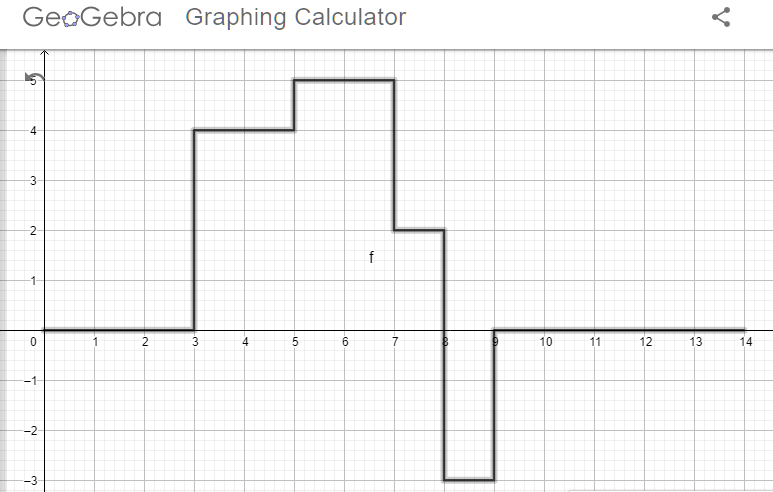
A1 – Superposition of two signals: The result of a superposition of two signals is a simple arithmetic sum of two functions. For the two signals shown in the question, the sum of two signals have value of 0 in the interval (0,3), then value of 4 (=2+2) in the interval (3,5), then value of 5 (=3+2) in the interval (5,7), then value of 2 (=3-1) in the interval (7,8), then value of -3 (=-2-1) in the interval (8,9), and finally a value of 0 in the interval (9,14). Running the command “Polyline({(0,0),(3,0),(3,4),(5,4),(5,5),(7,5),(7,2),(8,2),(8,-3),(9,-3),(9,0),(14,0)})” in GeoGebra yields below plot.

Q2 – [Adapted from Physics 10 Chapter 6 Assignment] Below video illustrates and explains Chladni plates, which can be used to visualize 2-dimensional standing waves.

Give a description of Chladni plates in their operation. What features stand out? Compare and contrast 2-dimensional standing waves illustrated with Chladni plates with 1-dimensional standing waves you have seen in Chapter 16 and 17 (and lab).
What do you think the boundary condition for the standing wave is at the edge of the Chladni plate? Give supporting evidences for your educated guess.

A2 – Chladni Plates: This is a relatively open-ended question. It is possible to give different takes on the same information presented in the video.

One way to describe the difference between the 2-dimensional standing waves illustrated on Chladni plates from the 1-dimensional standing waves seen on a wave on a string is in terms of nodes. For 1-dimensional standing waves, nodes are points (usually regularly spaced). The geometric shapes of the 2-dimensional standing waves are described in terms of nodal lines, the spots on Chladni plate where the sands gather, because these spots on the plate are not vibrating, allowing sand grains to gather at these spots. While the 2-dimensional standing waves are more complex (with “intricate” geometric designs appearing on the plates), these resonances only occur at specific frequencies, similar to the specific resonance frequencies which occur for 1-dimensional standing waves, and shorter distance between nodes (matching to shorter wavelengths) are associated with higher resonance frequencies. (And there are other features that might be mentioned—and not all these features need to be mentioned in a correct answer.)
The shape of nodal lines is complicated. When you look at the shapes forming on the circular Chladni plate, you see the clearest evidence that you have antinodes along the edge (look for the concentric-circle pattern; the distance between the edge and the outermost nodal line is about at half the distance between the nodal lines, which would place the edge right at the antinodes). However, on all Chladni plates, you do see nodal lines terminating at the edges, so it is possible to have nodes along the edge, and the boundary conditions go beyond simply specifying the edge as “antinode” or “node” (unlike with 1-dimensional standing waves).

Q3 – [Adapted from OpenStax, Chapter 17, Question 26] Describe what a “sonic boom” and a “shock wave” are. What conditions are needed to produce sonic booms and shock waves? What are examples of sonic booms and shock waves?
You might find following videos from a related Physics 10 assignment useful:

A3 – Sonic booms and shock waves: Sonic booms and shock waves are closely related. “Shock wave” is the more general term used for the waves that are produced by a source which is moving faster than the speed of the wave. In the context of sound waves, when an object moves faster than speed of sound, the object produces a shock wave (you can analyze this as a result of wave interference; movement of a sound source faster than speed of sound creates lines along which constructive interference occurs, resulting in the loud shock wave). “Sonic boom” is the phrase used for the shock wave produced by supersonic airplanes. The wave fronts of the shock waves of supersonic airplanes build up to a very large amplitude and creates a loud sound (“boom”) on the ground. As an aside, this loud sound is the reason for regulations around supersonic airplanes (… reconsideration of which has been in the news lately).

Coda

[ARCHIVAL NOTE: Below is the content of “Note on Peer Review” Canvas page]

The next Module item is your first peer-graded assignment, which covers conceptual questions from Chapters 3 and 4 topics. You will get the hang of these assignments as you complete the first few (and complete the peer reviews, which will give you some idea of what your peers will see, when they review your work).

To briefly summarize the peer review process:

In the morning (at 8 a.m.) after the conceptual questions are due (at 11:59 p.m.), your submission will be assigned to three of your peers to review, complete the rubric, and to leave helpful comments.
The review is not done anonymously, so please remember to be kind to each other. Also, the peer reviewer cannot see any comments other than their own, so within the peer review system, the direction of communication goes only one way.
Finally, there is a “Peer Review” assignment item at the end of the weekly module which briefly describes the process, as well as provides the model answers to aid in leaving helpful comments.

Below video from Spring 2024 Physics 4A virtual class session also goes over these (and a little bit more) aspects of the peer review.